Observe that, as well as the symmetries e, h
as for the parabola P, the ellipse E also has the
symmetries v, reflection in the y-axis, and r, the
half-turn about the origin. Again, these are clear
from the algebra, since if (x,y)εE, then we have
x2/a2 + y2/b2 = 1, so that we also have
(x,-y),
(-x,y)
and (-x,-y) on E.
Again, we will assume that there are no other
symmetries, so that the symmetry group of E
is {e,h,v,r}.
These symmetries are very useful in sketching.
Once we know the shape of the part of E which
lies in the first quadrant - {(x,y) : x, y ≥ 0}, we
can infer the rest of the curve by reflecting, first
in the y-axis - to get the top half, and then in the
x-axis to get the rest.
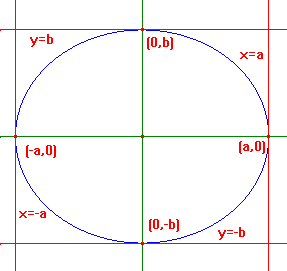
Note that the points (a,0),(-a,0),(0,b),(0,-b) are on E.
| Suppose (x,y)εE, so that | x2/a2 + y2/b2 = 1 |
| i.e. | x2/a2 = 1 - y2/b2 |
| then | x2/a2 ≤ 1, as y2/b2 ≥ 0 |
| i.e. | -a ≤ x ≤ a |
Similarly, E lies between the lines y = -b and y =b.
To get the shape of the portion of the curve in the
first quadrant, we could plot some points. The reader
familiar with differentiation will find a more formal
treatment for the ellipse and hyperbola here
Finally, we get the picture on the right. The ellipse E
is shown in blue. The green lines are the axes of
symmetry. The red lines form the "box" within which
E lies. They are tangents to E.
some further notation
The centre, O, of the half-turn is known as the
centre of the ellipse.
Each of the axes of symmetry cuts E in two points,
but the chord on the axis has length 2a, so is longer
than that on the y-axis, which has length 2b. Hence,
the x-axis is called the major axis of the ellipse, and
the y-axis is called the minor axis of the ellipse.