Wilson Stothers' Cabri Pages

The Proof of the Converse of Pascal's Theorem Pascal's Theorem Suppose that no three of the points A,B,C,D,E, are collinear. If the point F lies on the conic determined by A,B,C,D and E, then X = ACnDB, Y = CFnBE, Z = FDnEA are collinear. The Converse Suppose that no three of the points A,B,C,D,E, are collinear. If X = ACnDB, Y = CFnBE, Z = FDnEA are collinear, then the point F lies on the conic determined by A,B,C,D and E. Proof of the Converse Let C be the conic through A,B,C,D,E.
Suppose that CF = CY meets C at G, so CF = CG.	We show that F = G, so F is on C.
Now apply Pascal's Theorem to A,B,C,D,E,G to get	These are all on the conic C.
X = ACnDB, Y = CGnBE, W = GDnEA collinear,	CGnBE = Y as CG = CF
so that XY meets EA in W.
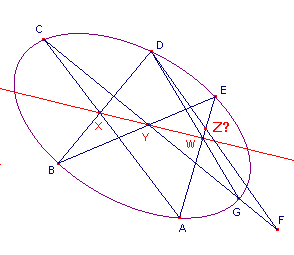
By hypothesis, X, Y and Z = FDnEA are collinear, so that XY meets EA in Z.
Hence W = Z.	XY, EA meet only once
Now CY meets DZ in F,	Definition of Z
and CY meets DW in G.	Definition of W
W = Z, so DW = DZ and hence F = G.
Note The diagram is a little puzzling. It purports to show a case with F not on C. But then the diagram indicates that X,Y and Z cannot be collinear, as X,Y,W are. As the proof shows, the only way to resolve this is to have W = Z, so that F = G.