Suppose that ABC and PQR are h-triangles.
Then there is a hyperbolic transformation t which maps
A to P,
B to B' on the h-line PQ, on the same side of P as Q, and
C to C' on the same side of the h-line as R.
Note that, as t preserves angle and hyperbolic distance,
d(A,B) = d(P,B'), d(A,C) = d(P,C'), d(B,C) = d(B',C'), and
<ABC = <PB'C', <BAC = <B'P'C', <ACB = <PC'B'.
If h-triangles ABC and PQR have
| (1) <ACB = <PRQ, |
| (2) <ABC = <PQR, and |
| (3) <BAC = <QPR, |
If any pair of sides have equal hyperbolic length, then the
h-triangles are h-congruent by the (ASA) condition.
Assume that no two are equal (we will obtain a contradiction).
Let t be the transformation implied by the Basic Strategy.
Then B' lies on the h-line PQ.
By the Basic Strategy, <BAC = <B'PC'.
By (3), <BAC = <B'PR, so C' lies on PR.
By the Basic Strategy, <ACB = <PC'B'.
By (1), <ACB = <PRQ, so <PC'B' = <PRQ.
By the Basic Strategy, <ABC = <PB'C'.
By (2), <ABC = <PQR, so <PB'C' = <PQR.
By our assumptions, C' lies on PR, but C' ≠ R,
and
B' lies on PQ, but B' ≠ Q.
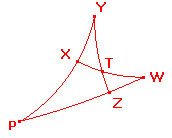
Thus X and Y are the points C' and R in some order,
with the angles at X and Y equal.
Also Z and W are the points B' and Q in some order,
with the angles at W and Z equal.
We have one of the two situations shown on the right.
In the top case, <PXT is an exterior angle of XYT,
but it is equal to <PYT, a contradiction.
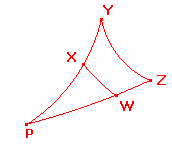
In the second case, the convex h-quadrilateral XYZW has
<WXY = π - <PXW = π - <PYZ ,and
<XWY = π - <PWX = π - <PZY.
Thus XYZW has angle sum 2π, again a contradiction.