The points of the boundary C do not belong to the plane. As we shall see, these
boundary points play a role similar to that of the "points at infinity" in euclidean
geometry. In different texts, these are known as the asymptotic, ideal, limit or
omega points of the geometry. We shall use the first of these.
definition
In the poincare disk model, the asymptotic points are the points of the circle C.
The extended disk E consists of the disk D together with the boundary C.
When we need to make it clear that we are dealing with a point of D, we shall
refer to it as an ordinary point.
A hyperbolic line H is the intersection of D with an i-line H* orthogonal to C. The
i-line cuts C in two points. These are the asymptotic points associated with H. To
avoid clumsy terminology, we shall treat them as points of H.
When we wish to emphasise that the asymptotic points are included, we shall
refer to the complete hyperbolic line H.
Likewise, a hypercircle "has" two asymptotic points, and a horocycle one.
A hyperbolic transformation h is the restriction to D of an inversive transformation
h* which maps D to D and C to C.
The latter shows that h* maps each asymptotic
point to an asymptotic point. Again, we shall not distinguish h* and its restriction to
D, and simply say that h acts on the asymptotic points.
Note. We have looked at the action of H(2) on C by itself in weird geometry.
Theorem HA1
If A,B are distinct points of E, there is a unique hyperbolic line through A and B.
proof
As A,B are in E, they are not inverse with respect to C.
The result follows immediately from Theorem O1.
definitions
If A is in D and X on C, then the h-ray AX
is the arc AX of the hyperbolic line through
A and X guaranteed by the theorem.
For A, B in D, the h-ray AB is the h-ray AX of the hyperbolic line AB which contains B.
The theorem also allows us to define the hyperbolic triangle ABC for any A,B,C in E.
definition
The hyperbolic triangle ABC is singly (doubly, trebly) asymptotic if one (two,
three) of the vertices lie on C.
Observe that, if A is an asymptotic point, the hyperbolic lines AB, AC are
orthogonal to C, so that The angle BAC is zero. It follows that the sum of
the angles of a trebly asymptotic triangle is zero, and its area is π. Also,
the sides AB, AC are of infinite hyperbolic length.
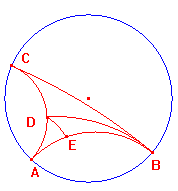
The sketch shows a trebly asymptotic triangle ABC, two doubly asymptotic
triangles ABD, BCD, and two singly asymptotic triangles ADE, BDE.
Theorem HA2
The sum of the angles of a hyperbolic triangle is less than π.
For triangles which are singly or doubly asymptotic this can be proved by
mapping an ordinary vertex to O, and proceeding as for a non-asymptotic
hyperbolic triangle.
Since asymptotic triangles have some sides of infinite length, we cannot
expect the full range of hyperbolic trigonometric results.
If ABC is a singly asymptotic triangle, with A on C, d(B,C) = l, <ABC =½π,
<ACB = γ, then tan(γ) = 1/sinh(l), i.e. sinh(l) = cot(γ).
proof
Take B' on the hyperbolic segment AB, and let d(B,B') = l', <BCB' = γ'.
Applying the tangent formula to triangle BB'C,
tan(γ') = tahn(l')/sinh(l).
As B' tends to A, l' tends to ∞, so tanh(l') tends to 1, and γ' tends to γ.
The result follows.
This may be viewed as the asymptotic analogue of the tangent formula.
Using standard formulae from trigonometry and hyperbolic trigonometry,
we can deduce that cosh(l) = cosec(γ), tanh(l) = cos(γ).
As an exercise, the reader may verify that the result may be restated as
tan(½γ) = exp(-l). This is Lobachevski's Formula.
The same limiting argument for a general singly asymptotic triangle when
applied to the Second Cosine Rule gives
Theorem HA3
If ABC is a singly asymptotic triangle with A on D, d(B,C) = l, <ABC = β,
<ACB = γ, then sin(β)sin(γ)cosh(l) = 1 + cos(β)cos(γ).
A standard trigonometric identity shows that this is equivalent to the earlier
result when β = ½π.