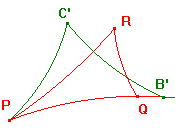
Suppose that ABC and PQR are h-triangles.
Then there is a hyperbolic transformation t which maps
A to P,
B to B' on the h-line PQ, on the same side of P as Q, and
C to C' on the same side of the h-line as R.
By the Interchange Theorem, there is an h-inversion u mapping A to P.
Suppose that u maps B to B1, and C to C1.
Now let v be the h-inversion in the h-line V bisecting <B1PQ.
As P is on V, v fixes P. By the choice of V, v maps B1 to a point B'
on PQ on the same side as Q.
Suppose that v maps C1 to C2.
If C2 is on the same side of PQ as R, we take t = vou so C' = C2.
If C2 is on the opposite side of PQ from R, let w be h-inversion in PQ.
Then w fixes P and B' (as they lie on PQ).
Suppose that w maps C2 to C'. This lies on the same side of PQ as R
since it lies on the opposite side from C2.
In this case, we take t = wovou.