a disc model for euclidean geometry

Some students find it difficult to accept that a geometry with a disc model can contain lines of arbitrary length. One way to appreciate that this can happen is to look at a disc model for the familiar euclidean geometry.

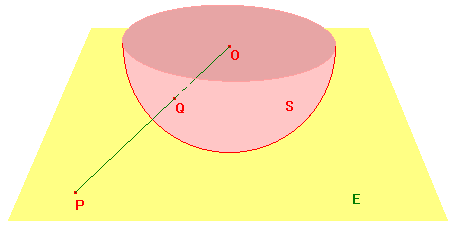
Let E be the usual model of the euclidean plane, and let S be the lower half of a sphere (centre O) touching E, with the "rim" deleted. For any P on E, let t(P) = Q, the point where OP cuts S. This defines a bijection t from E to S, so we can regard the finite surface S as a model for euclidean geometry.
If we now view S from directly above O, we get a model for the euclidean plane on a disc centred on O. Of course, the model "distorts" distances and angles on E.	In fact, a line on E through the point vertically below O is represented by a diameter of the disc!