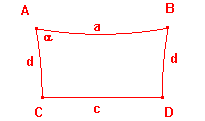
horocycles
We first met horocycles in our discussion of cyclic triangles. They reappear in the
study of our strange mapping. We also show that, if H is a horocycle at XεC, then
any hyperbolic line through X is an axis of symmetry - a diameter. If A and B lie on
a horocycle, then A,B divide into a finite and two infinite arcs. These behave like the
minor and major arcs of a circle. We prove the relevant results. We also give a
characterization of horocyclic polygons - this is really part of the major result. Finally,
we prove a formula for the length of a finite arc of a horocycle.
The sketch shows a horocycle H at the boundary point X.
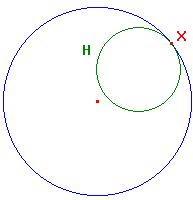
In our discussion, these appear first as part of the class of curves for which ptolemy's
theorem holds. They are intersections of i-lines with the disk. As with horocycles, points
A,B on a hypercircle divide it into a finite and two infinite arcs. Once again there are
similar results to those for circles and horocycles. Hypercircles also occur in the
major result on hyperbolic polygons. Also, any hyperbolic line which is orthogonal to
a hypercircle is an axis of symmetry - a diameter. The more interesting fact is that
they also occur when we attempt to mimic a euclidean construction for a line through
a point P parallel to a line L not through P. We define the locus C(P,L) as the set
{Q : P,Q an the same side of L and equidistant from L}. In euclidean geometry, this
produces the line through P parallel to L. In hyperbolic geometry it is a hypercircle.
The sketch shows a hypercircle H, defined using the hyperbolic line L.
Historically, these are significant as early pointers to the existence of hyperbolic geometry.
They arise by attempting to mimic the euclidean construction of a rectangle. Suppose we
have two points C,D on a hyperbolic line L and choose points A,B on the perpendiculars
to L at C,D respectively, and on the same side of L. In euclidean geometry, ABDC is a
rectangle - the angles at A and B are ½π, and |AB| = |CD|. In hyperbolic geometry, the
angles at A and B are equal, but acute, and d(A,B) > d(C,D). The figure ABDC is called
a saccheri quadrilateral. We prove the results mentioned above. We also prove
some other results about the size of the angles, areas, and the length of the arc of the
hypercircle through A and B associated with CD.