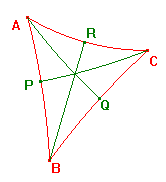
The internal angle bisectors of a hyperbolic triangle are concurrent.
Proof
By the Hyperbolic Sine Rule applied to the h-triangles AQC and AQB,
SImilarly, using the bisectors BR and CP,
Multiplying the ratios,
The angle bisectors all lie within the h-triangle, so any two must meet.
Let ABC be an h-triangle, and let the angle bisectors be AQ, BR and CP.
sinh(d(Q,C))/sin(<QAC) = sinh(d(A,Q))/sin(<ACQ), and
sinh(d(B,Q))/sin(<QAB) = sinh(d(A,Q))/sin(<ABQ).
As AQ bisects <BAC, <QAC = <QAB, so these equations yield
h(B,C,Q) = sin(<ACB)/sin(<ABC).
h(A,B,P) = sin(<CBA)/sin(<CAB), and
h(C,A,R) = sin(<BAC)/sin(<BCA).
h(A,B,P)h(B,C,Q)h(C,A,R) = 1.
Thus, by the Converse of Ceva's Theorem,
the bisectors AQ, BR and CP are collinear.
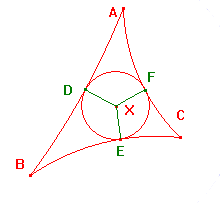
Suppose that X lies on the bisector of <BAC.
Then h-inversion in the h-line AX maps points on AB to points on AC.
Let the hyperbolic perpendiculars from X meet AB in D and AC in F.
Since h-inversion preserves angles, and h-perpendiculars are unique,
The h-inversion maps D to F, so d(X,D) = d(X,F).
Now suppose that X also lies on the bisector of <BCA. Then we also
have d(X,D) = d(X,E).
It follows that D, E and F lie on an h-circle C with h-centre X.
Finally, as XD is perpendicular to AB, C touches AB at D, and
similarly touches BC at E, and AC at F.