If P lies on the h-line AB, Q on BC and R on CA such that
h(A,P,B)h(B,Q,C)h(C,R,A) = 1,
and two of the h-lines CP, BR and AQ meet,
then all three are concurrent.
A little consideration shows that, if we change the labels of the vertices,
then either the factors are simply permuted, or are inverted and permuted.
Since our hypothesis is that the product is 1, the labelling of the vertices
of the h-triangle is immaterial.
The key is to show that the h-line through the intersection X of two of
CP,AQ,BR
and the third vertex cuts the third side of the h-triangle.
We apply Ceva's Theorem to this point X.
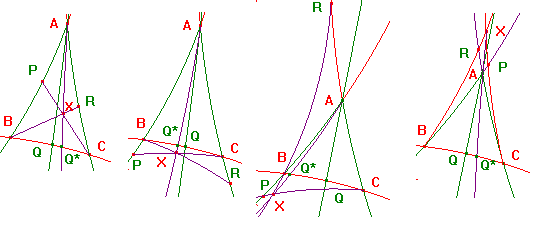 If P lies between A and B, then CP cuts the h-segment AQ, at X say.
If P lies between A and B, then CP cuts the h-segment AQ, at X say.
Also, BX cuts the h-segment AC, at R*,say.
Applying Ceva's Theorem to the h-triangle ABC, and the point X, we get
h(A,P,B)h(B,Q,C)h(C,R,A) = 1.
Comparing this with the hypothesis, h(C,R,A) = h(C,R*,A).
By the Hyperbolic Ratio Theorem, R = R*, so AQ,BR,CP concur at X.
A similar argument applies if R lies between A and C.
Now suppose that P lies beyond B, and R beyond C.
Then BR and CP meet at X, which lies within angle BAC.
Now AX cuts the h-segment BC at Q*, say.
It now follows as before that Q = Q*, so the h-lines are concurrent.
Next suppose that P lies beyond B, and R beyond A.
Then the h-ray RB enters angle PBC at B, and so cuts CP at X, say.
Since X lies within the angle BAC, AX cuts the h-segment BC, at Q*, say.
It now follows as before that Q = Q*, so the h-lines are concurrent.
The case where P is beyond A, and R beyond C is similar.
Note that, in all of the above cases, the h-lines AQ,BR,CP must meet.
We are left with cases where both P and R lie beyond A.
The hypotheses include the condition that at least two of AQ,BR,CP meet.
Suppose first that BR and CP meet, at X, say.
Then X lies within angle RAP, so AX meets the h-segment BC, at Q*, say.
It now follows as before that Q = Q*, so the h-lines are concurrent.
Suppose next that BR and AQ meet, at X, say.
Now X and C lie on opposite sides of AB, so CX meets AB, at P*, say.
Much as before, we deduce that P = P*, so the h-lines are concurrent.
The case where CP and AQ meet is similar to the previous case.
Note. There are cases where the h-lines are parallel or ultraparallel.
Note. Essentially the same argument works in the euclidean case.