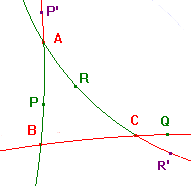
If P lies on the h-line AB, Q on BC and R on CA such that
h(A,P,B)h(B,Q,C)h(C,R,A) = -1,
then P, Q and R are h-collinear.
A little consideration shows that, if we change the labels of the vertices,
then either the factors are simply permuted, or are inverted and permuted.
Since our hypothesis is that the product is -1, the labelling of the vertices
of the h-triangle is immaterial.
The key is to show that an h-line through two of P,Q,R cuts the third side
of the h-triangle. We apply Menelaus's Theorem to this line.
Since the product is negative, at least one of the cuts is external.
Relabelling if necessary, we may assume that Q lies beyond C on BC.
If P lies on the h-ray AB, then the h-line QP cuts AC, at R* say.
Applying Menelaus's theorem to the h-triangle ABC, cut by PQR*,
we get h(A,P,B)h(B,Q,C)h(C,R*,A) = -1.
Comparing this with the hypothesis, h(C,R*,A) = h(C,R,A).
Then, by the Hyperbolic Ratio Theorem, R = R*, so P,Q,R are collinear.
There are two other possibilities:
If R lies on the h-ray CA, then the h-line QR cuts AB, at P* say.
The only other possibility is that P lies beyond A (e.g. at P'), and
that R lies beyond C (e.g. at R'). Then P'R' cuts BC, at Q* say.
In each case a similar application of Menelaus gives the result.
Note. Essentially the same argument works in the euclidean case.