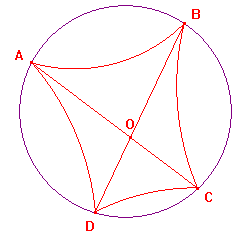
Since the hyperbolic quadrilateral is convex, the hyperbolic diagonals
intersect at an interior point. By the origin lemma we can map the
figure so that this is O, the centre of the disk. The result is shown in
the picture on the right.
Since O lies inside the hyperbolic quadrilateral, the sides bend "inwards".
Thus the euclidean quadrilateral contains the hyperbolic one. As the segments
AC, BD pass through O, they are euclidean segments also. Thus the two
diagonals are the same in either geometry. These meet, so the euclidean
quadrilateral ABCD is also convex.
We are now in a position to apply the euclidean version of ptolemy's theorem
to this euclidean quadrilateral. This says that |AC||BD| = |AB||CD|+|AD||BC|.
We now apply the distances theorem several times:
|AB| = s(AB)/c(OA)c(OB),
|BC| = s(BC)/c(OB)c(OC),
|CD| = s(CD)/c(OC)c(OD),
|AD| = s(AD)/c(OA)c(OD).
|AC| = s(AC)/c(OA)c(OC).
|BD| = s(BD)/c(OB)c(OD).
If we substitute these into the euclidean formula and cancel the c( ) factors,
we get our result.