Suppose that ABC and PQR are h-triangles.
Then there is a hyperbolic transformation t which maps
A to P,
B to B' on the h-line PQ, on the same side of P as Q, and
C to C' on the same side of the h-line as R.
Note that, as t preserves angle and hyperbolic distance,
d(A,B) = d(P,B'), d(A,C) = d(P,C'), d(B,C) = d(B',C'), and
<ABC = <PB'C', <BAC = <B'PC', <ACB = <PC'B'.
If h-triangles ABC and PQR have
| (1) d(A,B) = d(P,Q), |
| (2) <BAC = <QPR, and |
| (3) <ABC = <PQR, |
Let t be the transformation implied by the Basic Strategy.
Then B' lies on the h-line PQ.
By the Basic Strategy, d(A,B) = d(P,B').
By (2), d(A,B) = d(P,Q), so d(P,B') = d(P,Q), and hence B' = Q.
By the Basic Strategy, <BAC = <QPC'.
By (1), <BAC = <QPR, so C' lies on PR.
By the Basic Strategy, <ACB = <PC'B'= <PC'Q (as B' = Q).
By (3), <ACB = <PRQ, so <PC'Q = <PRQ.
If C' = R, we are done, as t maps ABC to PQR.
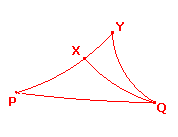
Otherwise, we have a picture like that on the right, where
X and Y are the points C' and R in some order and
<PXQ = <PYQ (as <PC'Q = <PRQ).
But <PXQ is an external angle of the h-triangle XYQ at X,
so must be greater than the interior angle <PYQ.
The contradiction shows that this case cannot arise.