If circle C with centre O is orthogonal to circle L with centre P,
then O lies outside L, and P lies outside C.
Proof
Suppose that C and L meet at the point A.
Let M be the tangent to C at A, and N the tangent to L at A.
As C is orthogonal to L, M is perpendicular to N.
Then N is perpendicular to M, the tangent to C at A,
so N passes through O. Thus O is outside L.
Similarly, P is outside C.

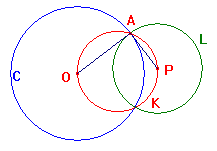
If P is a point outside the circle C, then there is a unique circle
with centre P orthogonal to C.
Proof
Let K be the circle on OP as diameter.
As P is outside C, K must cut C at
two points, A and B, say.
Let L be the circle, centre P, radius |PA|.
Being an angle in a semi-circle, <OAP is a right angle,
i.e. OA is perpendicular to PA.
Thus PA is tangent to C at A, and
OA is tangent to L at A,
so C and L are orthogonal.
The uniqueness is obvious, since, if C and L are orthogonal,
PA must be perpendicular to OP.