Apollonian Families

Apollonius of Perga is best remembered for his work on conics (he is responsible for the names parabola, ellipse and hyperbola), but he also investigated other
families of curves. One such has particular relevance to inversive geometry.

Definition
If A and B are points in the euclidean plane, and k is a positive constant,
then the apollonian curve Ak(A,B) is defined as the locus

{P : |PA| = k|PB|}
and A(A,B) as the apollonian family {Ak(A,B) : k > 0}.

If we choose k = 1, then we get the perpendicular bisector of AB, i.e. a line.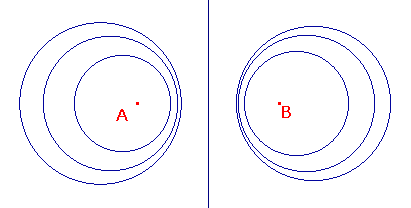
The sketch on the right shows some other possibilities.
Apollonius Theorem
  • Ak(A,B) is a line if k is 1, and a circle if k is not 1.
  • A and B are inverse with respect to Ak(A,B).
  • If A and B are inverse with respect to an i-line L,
    then L = Ak(A,B) for some k.

Proof of Apollonius Theorem

Notice that the first part of the theorem, shows that each family A(A,B) contains
many circles and one line. This is additional evidence for putting lines and circles
in a single class.

We use complex numbers as "coordinates" (so the point (a,b) in R2
is described by a + ib). Then the i-line Ak(A,B) has equation

|z -a| = k|z - b|,
where A, B have coordinates a, b.

For typographical reasons, we will use z* to denote the complex conjugate of z.

Immediately we see that inversion in the i-line given by the real axis + Ñ is
reflection in the real axis, i.e. maps z to z* (and Ñ to itself).

This is a fuller form of the theorem
than usually appears in texts.
But the proof is fairly short.

Inversion in the i-line |z| = r is also easy to describe,
it maps z to r2/z* (non-zero z), and interchanges 0 and Ñ.

An easy proof

We are now in a position to give a much neater proof that inversion maps i-lines
to i-lines. As a bonus, we get information about the images of inverse points.

The Second Inversion Theorem

Suppose that L and C are i-lines, and that t denotes inversion with respect to C.
Then t(L) is an i-line, and if A and B are inverse with respect to L,
then t(A) and t(B) are inverse with respect to t(L).

Proof of The Second Inversion Theorem

Main inversive page