This is given by the angle of rotation about P which maps PB to PB'. If we choose
the angle θ in the range (-π,π], then it is unique, and has a size |θ|, and also an
orientation, counterclockwise if θ > 0, and clockwise if θ < 0. The angle of size 0
has no orientation.
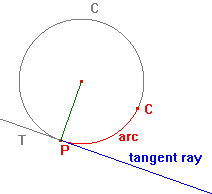
Suppose that A = PC is an arc of a curve C, and that there is a unique tangent T
to C at P. Then we can associate with the arc A a tangent ray at P - the part of T
in the direction implied by the arc. The sketch shows a case where C is a circle.
The arc is shown in red, the tangent ray in blue. The entire circle and the tangent
line are in grey.
Note that, in the case of a circle, the tangent ray is perpendicular
to the radius through P. This is shown in green.
Now suppose that two curves C and C' meet at the point P, and that A = PC and
A' = PC' are arcs on the curves. Then the tangent rays define an angle which we
will call the angle between the arcs.
If we consider the rotation which maps the
ray associated with A onto that associated with
A', then the angle has a unique
value θ in the range (-π,π].
This is illustrated in the lower sketch on the right.
Notes
(1) We chose the rotation mapping A onto A', so the order is important, so we
should refer to the angle defined by PC and PC' in that order. the angle defined
by PC' and PC will then be -θ. Often we are only interested in the size of the
angle, in which case the order is immaterial.
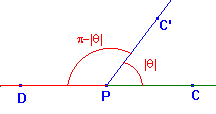
(2) If we choose a different arc PD on C so that this gives the opposite ray on
the tangent T, then we will get an angle related to θ
- it will be θ-π if θ ≥ 0, and
θ+π otherwise. The sketch below shows an example. The sizes of the angles
are
indicated. It is clear that the orientations are opposite since we map PC or
PD onto PC'.
(3) If the curves have a common tangent at P, then the angle will be either 0 or π
depending on the choice of tangent rays on this common tangent.
(4) If two arcs make an angle ±π/2, then the curves are said to be orthogonal at P.
In the case of two circles, or a circle and a line, then, by symmetry, the angles at
their intersections are of equal size (but opposite orientation). Thus, we can omit
mention of the point P and just say that the curves are orthogonal.

To investigate the effect of inversion on angles in an algebraic fashion we find it
useful to begin by looking at families of i-lines with a common tangent.