Apollonius of Perga
is best remembered for his work on conics (he is responsible for the names parabola, ellipse and hyperbola), but he also investigated other
families of curves. One such family has particular relevance to inversive geometry.
Definition
If A and B are points in the euclidean plane, and k is a positive constant,
then the apollonian curve Ak(A,B) is defined as the locus
{P : PA = k.PB}
and A(A,B) as the apollonian family {Ak(A,B) : k > 0}.
If we choose k = 1, then we get the perpendicular bisector of AB, i.e. a line.
Indeed, for any line L, we can choose A not on L and B the reflection of A in L,
so L is an apollonian curve.
The sketch on the right shows some other possibilities. | 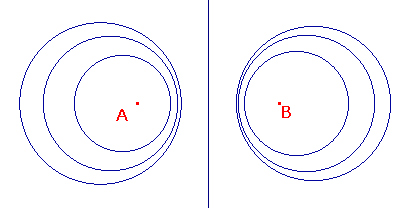
|
Observe that the members of an apollonian family are disjoint, for if a point P
lies on Ak(A,B) and on Ak'(A,B), then we have
PA = k.PB = k'.PB so k = k'.
Apollonius's Theorem
- Ak(A,B) is a line if k is 1, and a circle if k is not 1.
- If Ak(A,B) is the circle C with centre C and radius r, then
- A, B and C are collinear, with A and B on the same side of C, and
- CA.CB = r2.
- If A, B, and the circle C satisfy (1) and (2), then C is in A(A,B).
Proof of Apollonius Theorem
Notice that the theorem, shows that the set of all apollonian curves consists
of the set of circles and lines on the plane. Each family contains one line, so
we are associating each line with a family of circles.
We shall return to this presently.
We have already observed that, if the line L is in A(A,B), then
B is the reflection of A in L (and vice versa).
The second part of the Theorem shows that the points A and B are related to the circle in a similar way.
|
|
Definition
Suppose that C is a circle with centre O and radius r,
and that P is any point other than O.
Then the inverse of P with repsect to C is the point P' such that
(1) P' lies on the ray OP, and
(2) OP.OP' = r2.
We denote the inverse by iC(P), or, if C is obvious, by P'.
|
P' lies on the ray OP is equivalent to
O, P and P' are collinear, and
P and P' lie on the same side of O.
|
Parts two and three of the theorem may be restated as
A circle C belongs to the apollonian family A(A,B) if and only if
B is the inverse with respect to C (and vice versa).
Apollonian families have many nice properties. we shall return to some of these
after we have investigated inversion more fully.
|




