


|  |
Touching Circles
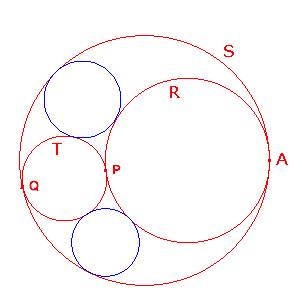
| In the introductory page, we mentioned a problem about circles touching three mutually tangent circles. We are now in a position to give a proof.
Theorem
If three circles R, S and T touch at A, P and Q as shown,
Of course, the proof consists of inversing in a circle |
 |
|
Proof
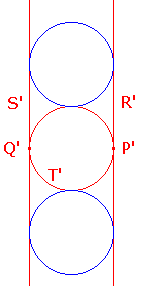
Let C be a circle with centre A. Inverting in C sends A to Ñ, so R and S map to extended lines R' and S'. As A is not on T, T must map to a circle T' touching R' at P and S' at Q'.
Any circle touching R' and S' must be have its center Inverting again in C, we get the circles touching R, S and T. |
 |
| Main inversive page |