If the point X does not lie on any side of ΔABC, and
AB meets CX in P, BC meets AX in Q and CA meets BX in R,
then
(AX/XQ) = (AP/PB) + (AR/RC),
(BX/XR) = (BP/PA) + (BQ/QC),
(CX/XP) = (CQ/QB) + (CR/RA).
Proof
Applying Menelaus's Theorem to Δ AQC, we have
(AX/(XQ)(QB/BC)(CR/RA) = -1.
Applying Menelaus's Theorem to Δ AQB, we have
(AX/(XQ)(QC/CB)(BP/PA) = -1.
Using the obvious facts about signed ratios :
(UV/VW) = -(VU/VW) = -(UV/WV) = 1/(WV/VU),
the equalities yield :
(AX/XQ)(BQ/BC) = (AR/RC),
(AX/XQ)(QC/BC) = (AP/PB).
Adding these and noting that
(BQ/BC) + (QC/BC) = ((BQ+QC)/BC) = 1,
we have the first of the required results.
The others are obtained by relabelling the figure.
Corollary
If X is the centroid of ΔABC, then
(AX/XQ) = (BX/XQ) = (CX/XP) = 2.
These follow at once since AQ, BR, CP are the medians,
so that (AP/PB) = (BQ/QC) =(CP/PA) = 1.
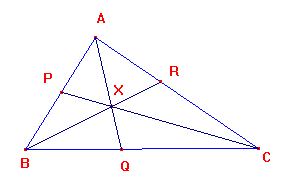
If the point X lies inside ΔABC, then AB meets CX in P,
BC meets AX in Q and CA meets BX in R, such that
(AX/XQ) + (BX/XR) + (CX/XP) ≥ 6.
Equality occurs if and only if X is the centroid of ΔABC.
Proof
Applying the above theorem
(AX/XQ)+(BX/XR)+(CX/XP)
= (AP/PB)+(AR/RC)+(BP/PA)+(BQ/QC)+(CQ/QB)+(CR/RA).
Now, (AP/PB)+(BP/PA) = (AP/PB) + 1/(AP/PB),
and there are two other such pairs in the above sum.
It is easy to see that for positive x, x + 1/x ≥ 2,
with equality if and only if x = 1 - see right.
Thus, (AX/XQ) + (BX/XR) + (CX/XP) ≥ 6,
with equality if and only if (AP/PB) = (BQ/QC) = (CR/RA) = 1.
The condition is equivalent to P, Q, R being the mid-points of
the sides of ΔABC. Then X is the centroid.
Then
x + 1/x -2
= (x2+1-2x)/x
= (x-1)2/x
≥ 0 with equality
if and only if x = 1.