The Klein View of Geometry

The euclidean group

Let E denote the euclidean plane.

Definition 1
An isometry is a transformation of E which preserves (euclidean) distance.
The set of all isometries is the euclidean group E(2).

Obvious examples are

t_A - the translation taking the origin O to the point A,
r_A(q) - rotation through q about the point A,
r_l - reflection in the line l.

By the Cosine Rule, the size of the angles of a triangle are determined by the lengths of its sides,
so isometries preserve the size of angles.

Definition 2
An isometry which preserves size and sense of angles is direct,
One which reverses the sense of all angles is indirect.
The set of direct isometries forms the subgroup E⁺(2) of E(2).

Translations and rotations are direct, while relections are indirect.
It is by no means clear that each isometry is either direct or indirect. We shall get this from Theorem 1 below.

Lemma 1
Suppose that t is an isometry which fixes the points O(0,0) and X(1,0). Then either

t is the identity, or

t = r_x (reflection in the x-axis).

Proof of the Lemma

Theorem E1
The group E(2) is generated by reflections.

Proof of Theorem E1

Each reflection is indirect, so if an isometry is the composite of an even number of reflections, it is direct,
if it is the product of an odd number, it is indirect. Thus, we have the

Corollary
Each isometry is either direct or indirect.
To give an algebraic description of E(2), it is convenient to regard E as the complex plane C.
Of course, the point with coordinates (a,b) is represented by the complex number a + ib.
Then translation and rotation about 0 (i.e the "origin") are particularly simple.
Note. For technical reasons, we shall denote the complex conjugate of z by z*.

t_A(z) = z + a, where a is the complex number representing A,
r₀(q)(z) = e^iqz. See the sketch on the right.
r_x(z) = z*.

We can now describe the elements of E(2).

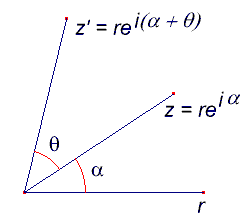Theorem E2
If t is a direct isometry, then t(z) = az + b, where a, b are in C, and |a| = 1.
If t is an indirect isometry, then t(z) = az* + b, where a, b are in C, and |a| = 1.

Proof of Theorem E2

Although Theorem E2 has a very simple form and proof, we often want to use coordinates.
Suppose that a, b are in C with |a| = 1.
Then a = cos(q) + isin(q), for some real q. Let b = c + id, with c,d real.

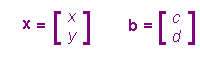
Suppose that t is the direct isometry t(z) = az + b.
If we look at real and imaginary parts of t(x +iy), then we see that
t maps the point (x,y) to the point (x.cos(q) - y.sin(q) +c, x.sin(q) + y.cos(q) + d).
Notice that this can be written in matrix form as x maps to A_qx + b,
with A_q as on the right.

Note that det(A_q)=1.

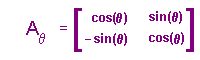Now suppose that t is the indirect isometry t(z) = az* + b.
A similar calculation shows that t maps (x,y) to (x.cos(q) + y.sin(q) +c, x.sin(q) - y.cos(q) + d).
Notice that this can be written in matrix form as x maps to B_qx + b,
with B_q as on the right.
Note that det(B_q)=-1.

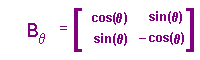
The matrices A_q and B_q comprise the group of orthogonal group of 2×2 real matrices.
It is not difficult to check that any matrix C which is orthogonal
(i.e. which satisfies C^TC = I) has one of these forms.

We now have a matrix version of E(2)

Theorem E3
E(2) = {t(x) = Ax + b, where A is a real orthogonal 2×2 matrix, and b a real vector}.
The direct isometries are those with det(A)=1.

Main Klein Page

Although Theorem E2 has a very simple form and proof, we often want to use coordinates. Suppose that a, b are in C with \|a\| = 1. Then a = cos(q) + isin(q), for some real q. Let b = c + id, with c,d real.
Suppose that t is the direct isometry t(z) = az + b. If we look at real and imaginary parts of t(x +iy), then we see that t maps the point (x,y) to the point (x.cos(q) - y.sin(q) +c, x.sin(q) + y.cos(q) + d). Notice that this can be written in matrix form as x maps to A_qx + b, with A_q as on the right.	Note that det(A_q)=1.
Now suppose that t is the indirect isometry t(z) = az* + b. A similar calculation shows that t maps (x,y) to (x.cos(q) + y.sin(q) +c, x.sin(q) - y.cos(q) + d). Notice that this can be written in matrix form as x maps to B_qx + b, with B_q as on the right.	Note that det(B_q)=-1.