cross-ratio is a ratio of signed ratios in Π (see the embedding theorem)
The Greeks studied this, thinking of the quantity as defined by a pencil
of four lines i.e. a set of four coplanar and concurrent lines. In projective
geometry, we regard the lines as representing collinear p-points, and the
common point as the origin
in the model RP2.
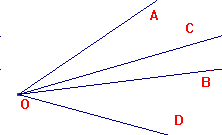
A particularly interesting case is when the cross-ratio is -1, when we say
that the pencil is harmonic. The image on the right shows such a pencil.
To show how information from a projective figure can be used to obtain
euclidean results, we begin with the following theorem.
A mid-point theorem
Suppose that A,B,C,D are p-points with (A,B,C,D) = -1, and that a
plane Π is chosen so that the p-points embed as A',B',C',D' with
(only) D' ideal. Then C' is the mid-point of A'B'.
From case (5) of the the embedding theorem, we have (A,B,C,D) = C'A'/C'B'.
Thus C'A'/C'B' = -1, so C' is the mid-point of A'B'.
We can rephrase this as a euclidean result:
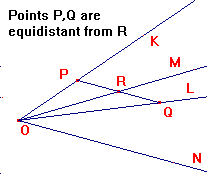
If (K,L,M,N) is a harmonic pencil and P,Q lie on K,L such that PQ||N,
then M bisects PQ.
To see how such a cross-ratio may arise in practice, we will look at some
results on projective conics.