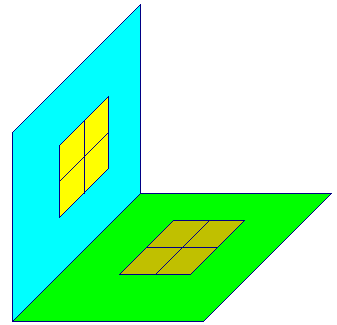
rectangular panes. The shadow on the floor will not, in general,
be rectangular. As the Sun moves, the shadow will change.
The basic problem of affine geometry is to determine what
properties do all of the shadows have in common.
As the Sun gets lower, shadows lengthen, so we see that
lengths are not invariant. Also, experience shows that the
shape of the shadow changes, so angles are not invariant.
On the other hand, we might observe that the shadows of
the rectangular panes are always parallelograms. This
suggests that parallelism is preserved.
Since the Sun is far from the Earth, a reasonable approximation
is to assume that the rays are parallel. This leads us to the idea
of a parallel projection.
For the moment, we observe that, provided the Sun's rays are
not parallel to either the wall or the floor, then each point in
the plane of the wall leads to a point in the plane of the floor.
In other words, we have a transformation of R2.
We will begin our study of affine geometry in the kleinian way,
starting with a group of transformations of R2. Later, we will
see that our "shadow transformations" actually generate the
entire affine group.