of plane figures, i.e. euclidean transformations which map the figure to
itself. From the kleinian view, there is no reason why we should restrict
attention to euclidean transformations.
Suppose that G is a group of transformations of a set S, so that G gives
a geometry on S. In this geometry, a figure F is simply a subset of S.
We may consider elements of G which map F to itself.
Definition
Suppose that G is a group of transformations of a set S, and that F is a
subset of S. An element g of G is a G-symmetry of F
if g(F) = F. The set
of G-symmetries of F is denoted by S(F,G).
This set contains much geometrical information about F, as we shall see.
Theorem SG1
If G is a group of transformations of a set S, and F is a subset of S, then
S(F,G) is a subgroup of G.
The subgroup S(F,G) is called the G-symmetry group of F. If H is any
subgroup of S, it also defines a geometry on S, and hence we have an
H-symmetry group S(F,H). Of course, the symmetry groups are related.
Theorem K3
If G is a group of transformations of a set S, H a subgroup of G, and F is
a subset of S, then S(F,H) is a subgroup of S(F,G).
Proof
Since S(F,H) is a group, by Theorem SG1, it is enough to show that it is
a subset of S(F,G).
Suppose that h is in S(F,H). Then h(F) = F. Since H is a subgroup of G,
we also have hεG. Thus hεS(F,G), as required.
At the moment, we can offer ony a rather contrived example to show that
the subgroups may be different, i.e. that S(F,H) may be a proper subgroup.
Example 1
Let F be the ray {(x,0) : x ≥ 0} in R2. Then it is easy to see that S(F,E(2))
contains only e, the identity, and r, reflection in the real axis. On the other
hand, S(F,S(2)) also contains the scalings sk(x) = kx, k > 0. Thus, S(F,E(2))
is a proper subgroup of S(F,S(2)).
Recall that two subsets F, F' of S are G-congruent if there is an element g
of G with g(F) = F'. Since the definitions of G-congruence and G-symmetry
are somewhat similar, it is not surprising that the concepts are related.
Theorem SG2
If F and F' are G-congruent subsets of S, then S(F,G) and S(F',G) are
conjugate subgroups of G.
Indeed, if gεG is such that F' = g(F), then
S(F',G) = gS(F,G)g-1.
will be isomorphic groups. Unfortunately, the converse is false. We can have
non-congruent figures with identical (and hence isomorphic) symmetry groups.
Example 2
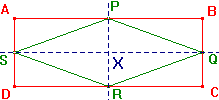
In the picture on the right, ABCD is a rectangle, and P,Q,P,S are the mid-points
of AB,BC,CD,DA respectively. Then the quadrilaterals ABCD and PQRS each have
E(2)-symmetry group K = {e,h,v,r},
where e is the identity, h and v are the
reflections in the lines SQ and PR, and r is the half-turn about X.
non-isomorphic G-symmetry groups must be incongruent in the G-geometry.