If P,Q,R are distinct points, then there is a unique line through Q making equal angles with
rays QP and QR (through R if R is on the ray QP) this is called the bisector of <PQR.
Here, we shall examine the cases in some more detail.
(1) R lies on the line QP, but not on the ray QP - so Q is between P and R.
Then the rays QP, QR make angle π.
A line through Q which makes equal angles with both must make angle π/2 with each
This must be the perpendicular to PQ at Q.
(2) R is on the ray QP.
Then the rays QP and QR coincide, so make zero angle.
There now appear to be two candidates - the line QP and the perpendicular to QP at Q.
We added the condition "through R" to select the former.
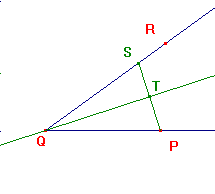
We need to know how the line can be drawn.
The sketch on the right shows a typical configuration.
By one of Hilbert's axioms, we can choose S on the ray QR with n(Q,S) = n(Q,P).
By (7) the segment PS has a midpoint T, so we have n(P,T) = n(T,S).
Now ΔQTP and ΔQTS have corresponding sides equal, so we can use (SSS) to show
that the ray QT is equally inclined to QP and QR as <PQT = <TQR.
Thus, QT is the required line.
NOTE the congruence also shows that <QTP = <QTS, so PS is perpendicular to QT.
We shall need the following result:
Suppose that the line L is the bisector of <PQR. Then rL(P) lies on the ray QR.
proof
In case (1), L is the line through Q perpendicular to QP.
Then rL(P) lies on QP, since this is perpendicular to L, and lies
on the opposite side of L to P. Thus it lies on the same side as R,
and so on the ray QR.
In case (2), L is the line QP, so rL(P) = P, and so is on QR.
In case (3), L is the line QT above. Now, we chose S as a point on the ray QR.
We showed also that QT is perpendicular to PS. Since also n(P,T) = n(T,S), we
see that rL(P) = S, so is on the ray QR.