
The Theorem of Dandelin
In the Main Conics Page, we define a conic in terms of the focus, directrix and eccentricity.Conics may also be defined as plane sections of a right circular cone.
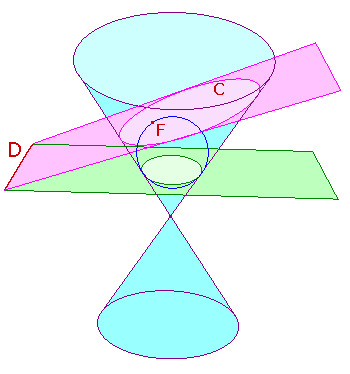
In the picture on the right, the pink plane cuts the pale blue cone in a curve C.
To show that the definitions are equivalent,
we need to produce a focus-directrix pair for C.
Imagine a sphere sitting inside the top sheet of the cone.
If we begin with a small sphere and dilate it, eventually it will touch the pink plane.
In the picture the blue circle is the outline of this sphere. It touches the plane at F.
This is known as a Dandelin
sphere for the conic section.
Using the symmetry of the cone about its axis,
the sphere will touch the cone along a circle in a plane perpendicular to the axis.
In the picture, this is the green plane.
If the cutting (pink) plane is also perpendicular to the axis,
then the section C is clearly a circle.
Otherwise, the cutting plane meets the green plane meet in a line D.
Then (it can be shown that) for each point P on C,
the ratio of the distance from P to F to that from P to D is a constant, e.
Thus, C is the conic with focus F, directrix D and eccentricity e.
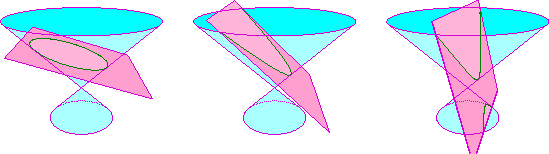
The picture below shows the three cases (ellipse, parabola, hyperbola)
You can find a proof in the case of an ellipse here.
A complete proof (in french) with nice graphics appears here.
The title "Les theoremes belges" refers to the fact that Dandelin and Quételet were Belgian.