
Poles, polars and duality - the geometrical approach
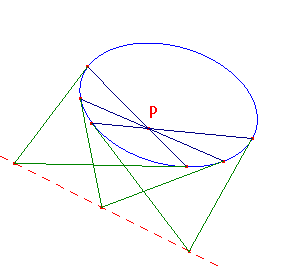 Key Theorem
Key Theorem
Suppose that C is a conic and that P is a fixed point.
If the chord AB of C passes through P, then the tangents at A and B meet on a fixed line.
Theorem 2 on the algebra page amounts to a proof of this.
Note that, if P is on C, then the line is the tangent at P
(since, for any point A on C, the tangents at A and P must meet on the tangent at P).
To allow us to state this theorem without the need for special cases,
we must allow ideal points
(also called
points at infinity).
With each direction on the plane (i.e. each class of parallel lines), we associate an
ideal point.
The set of ideal points is the ideal line or
line at infinity.
A detailed description is given on the ideal points page.
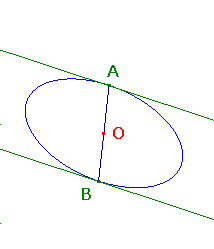
This allows us to unify classical theorems. For example,
The Parallel Chords Theorem
Suppose that C is a central conic
(an ellipse or hyperbola) with centre O.
If the chord AB of C passes through O, then the tangents at A and B are parallel.
In the language of ideal points,
this is just a special case of the Key Theorem
(the tangents meet on the ideal line).
Ideal points also allow us to give a definition of tangent purely in terms of incidence
(see Tangents and ideal points).
Poles and Polars
Provided we allow ideal points and lines, every point has a line associated with it by the Key Theorem.
Definition
Suppose that C is a conic, and that P is any point.
The polar of P with respect to C
is the line specified in the Key Theorem.
By the remark after the Key Theorem, if P lies on C, then the polar of P is the tangent at P.
The main result on polars is
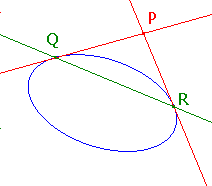 La Hire's Theorem
(this is illustrated with Cabri here)
La Hire's Theorem
(this is illustrated with Cabri here)
Suppose that C is a conic, and that P and Q are points.
Then P lies on the polar of Q if and only if Q lies on the polar of P.
Suppose that we can draw two tangents from the point P to the conic C,
and that these meet C in Q and R. (Such a point P is said to lie
outside C.)
Since the polars at Q and R are the tangents at these points, P lies on both polars.
Then, by La Hire's Theorem, Q and R lie on the polar of P, so
if P lies outside C, then the polar of P is the chord of contact QR.
Suppose that C is a conic and that L is a line. Choose points A and B on L.
Let P be the point of intersection of the polars of A and B.
Then, by La Hire's Theorem, A and B must lie on the polar of P,
so the polar of P is the line L.
Thus, every line is the polar of some point.
Definition
Suppose that C is a conic, and that L is a line.
The pole of L with respect to C
is the point with polar L.
Duality with respect to a conic C.
Suppose that C is a fixed conic.
Then we can define a map from
the set of points (including ideal points) and lines on the plane to itself as follows
if P is a point, then the line P' is the polar of P with respect to C,
if L is a line, then the point
L' is the pole of L' with respect to C.
If X belongs to the set, then X' is the dual of X with respect to C.
Of course, (X')' = X.
We say that a point and line are incident if the point lies on the line.
It is a consequence of La Hire's Theorem that duality preserves
incidence.
Indeed, La Hire's Theorem yields the following central result.
The Principle of Duality
If a theorem involves only concepts defined in terms of incidence,
then there is a dual theorem obtained by replacing
each object and each concept by its dual.
Suppose that F is a geometrical figure composed of points and lines.
Then the
dual of F with respect to C
is the figure F' consisting of of the polars of the points of F,
together with the poles of the lines of F.
For convenience, we define a polygon as either
an ordered list of points (a point-polygon), or
an ordered list of lines (a line-polygon).
For example, if the points A,B,C,D define the quadrilateral Q,
then Q may also de defined by the lines AB, BC, CD,DA.
If P is a polygon with n verices (and hence n sides), then so is P'.
Note that, since the objects are ordered, we can talk about, for example,
opposite sides of a polygon with an even number of sides.
In using the Principle of Duality, it is useful to have a table of duals of various concepts.
| concept | dual concept |
| point | line |
| line joining points | intersection of lines |
| collinear points | concurrent lines |
| polygon | polygon |
| vertex | side |
Now it is routine to write down the dual of any theorem. For example,
Pappus's Theorem Cabri illustration
If alternate vertices of a hexagon are
collinear,
then the intersections of
opposite sides are collinear.
This has as its dual
Brianchon's First Theorem Cabri illustration
If alternate sides of a hexagon are
concurrent,
then the lines joining
opposite vertices are concurrent.
 Using the traditional focus-directrix definition, we obtain a conic as a set of points
(a point-conic),
Using the traditional focus-directrix definition, we obtain a conic as a set of points
(a point-conic),
but we can equally well define a conic as the envelope of its tangents
(a line-conic).
The figure on the right shows a conic with a few of its tangents.
This indicates that the envelope of tangents to a conic is the conic itself.
In the language of duality,
for any conic C, the dual of C with respect to C is C itself.
The Dual Conic Theorem
Proof of the Dual Conic Theorem
Let C be a fixed conic.
We can now extend our table of dual concepts.
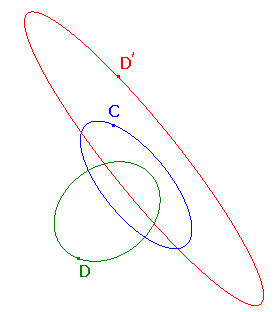 It is now natural to ask what happens when we look at the dual of a conic with respect to a different conic.
It is now natural to ask what happens when we look at the dual of a conic with respect to a different conic.
Suppose that C and D are conics.
Consider D as a line-conic.
Then D', the dual with respect to C, will be a set of points.
We can actually identify this dual as another conic, as the next theorem shows.
Suppose that C and D are conics.
Then the dual of D with respect to C is a conic.
Suppose that D is any conic, and that L is the polar of P with respect to D.
Choose A and B on D, so that P lies on AB.
Now apply duality with respect to C.
By the definition of polar,
the tangents TA and TB to D at A and B intersect on L.
Hence the line joining the points TA' and TB' must pass through L'.
Also, A' and B' are tangents to D' at TA' and TB'.
The chord (line joining) AB dualizes to the intersection of the tangents A' and B'.
and so lies on the line P' (as P is on AB).
Thus, L' is the pole of P' with respect to D'.
| concept | dual concept |
| point-conic | line-conic |
| point on conic | tangent to conic |
| pole | polar |
The Common Tangents Theorem
Proof of the Common Tangents Theorem
Since distinct conics intersect in at most four points,
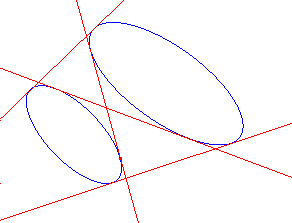 A nice application of the Dual Conic Theorem is to find any common tangents to two given conics.
A nice application of the Dual Conic Theorem is to find any common tangents to two given conics.
Suppose that C and D are distinct conics.
Then the common tangents (if any) to D and C
occur at the points
where C intersects the dual of D with respect to C.
there are at most four common tangents.