Tangents - a geometrical approach
The usual definition of a tangent to a curve is as the limiting position of a chord.
This assumes that the limit of the gradient exists.
Since a conic has an equation quadratic in the coordinates, the limit does exist.
Here we give a treatment without limits, showing that tangents can be defined purely in terms of incidence.
It also highlights the importance of ideal points.
An obvious first attempt would be the following
Temporary Definition
A line is a tangent to a conic if it meets the conic in only one point.
This works for an ellipse, but fails for parabolas and hyperbolas.
|
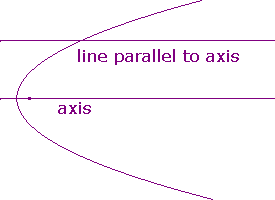
The Parabola Here, any line parallel to the axis cuts the curve once, but we would not describe it as a tangent. dummy
|
dummy |
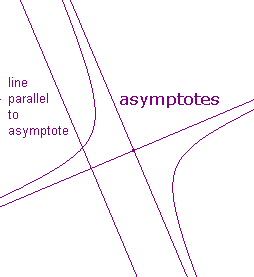
The Hyperbola Here, any line parallel to an asymptote cuts the curve once, but we would not describe it as a tangent.
|
Ideal points on a conic
We say that
Definition
Now each line parallel to the axis meets the parabola twice,
once as shown above, and again at the ideal point for this direction.
Note that the ideal line meets the parabola once so is a tangent at this ideal point.
Now each asymptote meets the hyperbola once, so is a tangent at the corresponding ideal point.
Other lines parallel to the asymptotes meet the hyperbola twice, once as above, and again at the ideal point.
The ideal line meets the hyperbola twice (at these ideal points), so is not a tangent.
A line is a tangent to a conic if it meets the conic in only one point,
real or ideal.
This can be justified either on the grounds of geometric intuition, or via the algebra.
In the latter approach, we note that ideal ponts correspond to points with homogeneous coordinates
[x,y,0].