Homogeneous coordinates

The introduction of ideal points provides many advantages,
but it means we can no longer represent a point by its cartesian coordinates.

To allow us to use algebraic methods to study the euclidean plane with ideal points,
we need a new model. We begin with a purely formal definition of a new geometry,
which we call RP2.

Definition 1
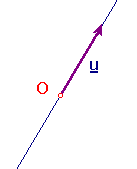
The set RP2 consists of all objects of the form [u] = {ku, k non-zero},
where u = (u,v,w) is a non-zero vector. The elements are RP2-points .
For any choice of k, the triple (ku,kv,kw) are homogeneous coordinates for U.

In other words, an element of RP2 is a line through the origin O in R3 (but with O deleted).
Note that [u] = [v] if and only if they give the same line, i.e. u=kv, for some non-zero k.

Definition 2
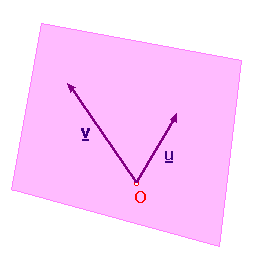
If U = [u] and V = [v] are RP2-points, then the RP2-line UV is defined to be
the set {ku + lv, k,l not both zero}

Then, in R3, UV is the plane through O generated by u and v (but with O deleted).

Thus an RP2-line has equation of the form ax + by + cz = 0.
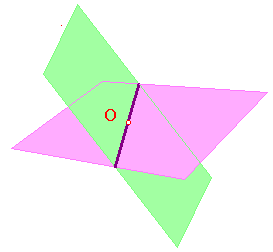Now suppose that L and M are distinct RP2-lines.
Then the defining planes in R3 intersect (since each is through O),
and so meet in a line through O, i.e. in an RP2-point.

Thus, the incidence rules for the geometry RP2 are,

two RP2-points define an RP2-line,
two RP2-lines define an RP2-point.

These are exactly the same as those of the euclidean plane with ideal points!
In fact the two geometries are very closely related indeed.

Let Ê denote the euclidean plane E, together with its ideal points.
As usual, we introduce x,y coordinates on E.

Now the clever bit - we think of E as lying on the plane z=1 in R3,
so the point (a,b) on E lies on (a,b,1).

Let P be the point (a,b) on E. Then P lies on the RP2-point [(a,b,1)]. Thus,
each point of E defines an RP2-point with non-zero third coordinate.

Now suppose that the lines L and M lie on E and are parallel.
As parallel lines on E, they must have equations ax + by + c =0 and ax + by + c' = 0.
It is easy to see that L and M are, respectively, the intersections of
ax + by + cz =0 and of ax + by + c'z =0 with z=1.
Now, where ax + by + cz =0 and ax + by + c'z =0 intersect, we have
ax + by = 0 and z=0. These define the RP2-point [(b,a,0)], so
each family of parallel lines on E defines an RP2-point with third coordinate zero.
But a family of parallel lines on E correspond to an ideal point of E, so
each ideal point for E defines an RP2-point with third coordinate zero.

Thus, the points of RP2 correspond to those of Ê.

Lines in RP2.

Let L be an RP2-line with equation ax + by + cz = 0.
  • if a and b are not both zero, then L meets z=1 in the line ax + by + c = 0, z=1,
    so L meets E in the euclidean line ax + by + c = 0.
    Also, L meets z=0 in the line ax + by = 0, z=0. This is the RP2-point [b,-a,0].
    In this case, L corresponds to a line of E, together with its ideal point.
  • if a=b=0, then L is z=0, so corresponds to the set of ideal points of E,
    i.e. to the ideal line for E.
Thus, the lines of RP2 correspond to the lines of Ê.

Conics revisited.

Let C be the solution set of the equation ax2 + bxy + cy2 +fxz +gyz +hz2 = 0.
If (x,y,z) is a solution, then so is (kx,ky,kz) for any non-zero k.
Thus, C is an object in RP2, i.e. a set of RP2-points.

We are interested cases where C does not contain an RP2-line.
If a=b=c=0, the equation is 0 = fxz + gyz + hz2 = (fx + gy + hz)z, so C contains z=0.
Thus, we may assume that a, b, c are not all zero.

As in the case of an RP2-line, we shall look at how C meets Ê by considering
separately its intersections with z=1 and with z=0.

  • C meets z=1 in the curve ax2 + bxy + cy2 +fx +gy +h = 0, z=1,
    i.e. C corresponds to the curve ax2 + bxy + cy2 +fx +gy +h = 0 on E.
    This is the equation of a conic on E.
  • C meets z=0 in the curve F(x,y)=ax2 + bxy + cy2= 0, z=0,
    There are three possible cases
    • F(x,y) does not factorize over R. Then C does not meet z=0.
      In other words, C gives rise to no ideal points for E.
    • F(x,y) = p(qx + ry)^2. Then C meets z=0 in [r,-q,0],
      a single RP2-point (which corresponds to one ideal point for E).
    • F(x,y)=(px + qy)(rx + sy). Then C meets z=0 in [q,-p,0] and in [s,-r,0].
      These correspond to two ideal points for E.

Thus, C gives rise to a conic on E plus 0, 1 or 2 ideal points.

It is not difficult to see that these correspond to an ellipse, a parabola and a hyperbola.
A proof can be obtained from these pictures.

Algebra Page Main Conics Page Main Cabri Page