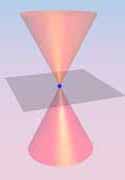
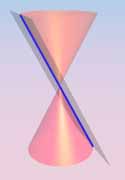
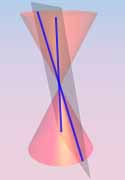
In this page, we show pictures of conics obtained as sections of a right circular cone. For completeness, we include the degenerate cases. Definitions Given a point V, a line L through V, and αε(0,π/2), the cone with vertex V, axis L and angle α consists of all points on lines through V making angle α with L. The lines are called the generators of the cone. As an example, take the origin O as vertex, the z-axis as axis, and α = π/4. This defines the cone K0 with equation x2+y2=z2. Sections of K0 by planes z = k (k ≠ 0) are circles.
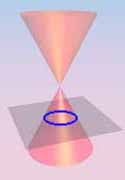
Intersections with planes not through the vertex are the usual plane conics. Note. It is far from clear that these are conics as described by the usual focus-directrix definition. The theorem of Dandelin shows this directly. Here, we will show that the sections of a cone have equations quadratic in x and y. Since we know that such curves are plane conics, this is enough. The equations of conic sections
	ellipse	parabola	hyperbola
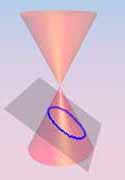
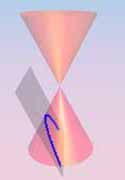
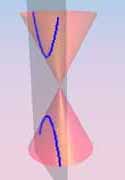
Intersections with planes through the vertex give degenerate plane conics. Observe that each is either finite (a single point!), or contains a line (a generator of K0). On the other hand, it is easy to see that no non-degenerate conic contains a line.
	point	line	line pair

main conics page