through three points A,B,C in the disk. The CabriJava applet should have indicated that
this is not always possible. This is easy to prove. Recall that a hyperbolic circle is also
a euclidean circle lying wholly within the disk. If A,B and C lie on a euclidean line, then
no such circle exists. Equally, if A,B and C lie on a hyperbolic line, then this is either part
of a euclidean line, or part of a euclidean circle K orthogonal to the boundary C. In the
former case, there is no circle, as before. In the latter case, K is the only circle through
the points, and it cuts C twice. Thus we do have cases with no hyperbolic circumcircle.
Here we identify the region R of the disk such that, for CεR, ΔABC has a hyperbolic
circumcircle. Obviously, the region will depend on A and B, and will exclude the euclidean
and hyperbolic lines AB.
It is difficult to identify the region within hyperbolic geometry. This is probably innevitable
since, as we shall see, the boundary consists of arcs which are neither hyperbolic lines
nor hyperbolic circles. The proof will use inversive tools.
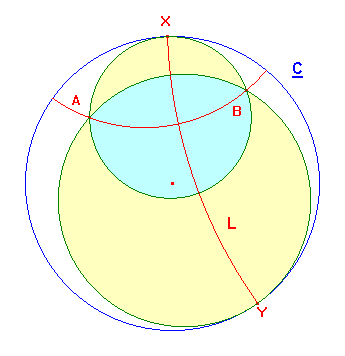
Suppose that A and B are distinct points in D.
Choose a circle K with euclidean centre A, and denote inverses with respect by dashes.
We observe that any line or circle through A and B inverts to a line through B'. We also
observe that C inverts to c circle C', centre Z'. C' does not contain B' since B is inside C.
The hyperbolic line AB is an arc orthogonal to C, it maps to a line through B', orthogonal
to C'. This must be the line B'Z'. This is illustrated
in the figures below.
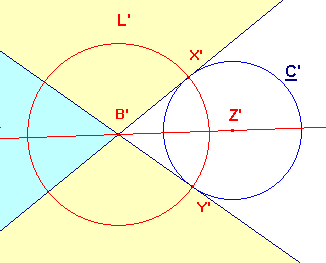
Now concentrate on the right hand figure. There are two lines though B' which touch C'.
Let the points of contact be X' and Y'. A line through B' which does not meet C' must lie
entirely in the yellow shaded regions. A little thought shows that these are the images of
the yellow regions in the left hand figure. Thus, the points C for which ΔABC does have a
hyperbolic circumcircle are precisely those in these regions.
The boundaries are arcs of the euclidean circles through A and B which touch C at X and Y,
the inverse images of X' and Y'. In fact, we can describe X and Y in hyperbolic terms.
Let L' be the circle, centre B' through X' (and hence through Y'). Clearly this is orthogonal
to C' and to the line B'Z'. It therefore inverts to the circle L through X and Y, orthogonal to
C and to the hyperbolic line AB. The first shows that the arc XY is a hyperbolic line. Inversion
in this line maps each of the green circles to themselves - look at the corresponding map
in the right hand figure. The inversion therefore interchanges the intersections, A and B.
It follows that the hyperbolic line XY is the hyperbolic bisector of the hyperbolic segment AB.
Thus, we could dispense with the right hand firure. The boundaries we require are arcs of
the euclidean circles through A,B,X, and through A,B,Y, where X and Y are the boundary points
of the hyperbolic bisector of AB. Indeed, they are the arcs which touch the boundary.
This leads us to define to a new concept:
Definition
A euclidean circle which touches C internally at a point X is a horocycle at X.
Note that, if M is a horocyle at X, then the set M-{X} lies in D, so is a figure in hyperbolic
geometry. However, since M neither lies within D nor is orthogonal to it, the figure is not
a hyperbolic line or circle.
Horocycles Theorem
(1) If M is a horocycle at X, and hεH(2), then h(M) is a horocycle at h(X).
(2) If A, B are distinct points in D, then there are two horocycles through A and B,
each meets C in a boundary point for the hyperbolic bisector of AB.
The first is easy - the image of M will be a circle lying within C, touching it at the image of X.
This means that horocycles are hyperbolic objects.
The proof of the second is contained in the above discussion.
With this language, we can now state the result we obtained above as the
Hyperbolic Circumcircle Theorem
For fixed A,B, a point C is such that there is a hyperbolic circle through A,B and C
if and only if
C lies in exactly one of the horocycles through A and B.
There is a CabriJava applet which illustrates the result.
We can also tackle the problem algebraically, characterizing the triangles which do
have a circumcircle in terms of the hyperbolic lengths of their sides.
A somewhat more detailed approach, with additional results appears in circumcircles