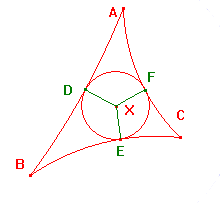
The internal angle bisectors of a hyperbolic triangle are concurrent.
As in euclidean geometry, the point of concurrence of the angle bisectors
is the centre of the incircle - a circle touching all three sides. Indeed, the
same proof suffices.
Proof of the angle bisector theorem and the incentre property
In euclidean geometry, we then look at excircles - that is to say circles which
touch all three sides of a triangle, but lie outside the triangle. These are best
by looking at external bisectors of the angles. If we try this in the hyperbolic
plane, we may find that the h-lines do not intersect, and no excircle exists.
CabriJava illustration of excircles
In these theorems, the h-segments all lie within the h-triangle, so that any two
must meet. Then the Converse of Ceva's Theorem gives an unconditional result.
In situations where two of the h-segments lie outside the h-triangle, we can
have cases where the product of the h-ratios is 1, but the h-segments do not
meet.
A simple example is that of (hyperbolic) altitudes.