The area of parallelograms and triangles follows easily from this definition.
The area of other regions is determined by a limiting process involving an
approximation by rectangles. In hyperbolic geometry, we do not have figures
analogous to rectangles. A hyperbolic quadrilateral has angle sum less than 2π
so cannot have four right angles. Instead, we use triangles as basic figures.
the gauss-bonnet formula
If the hyperbolic triangle ABC has angles α, β,γ, then its area is π-(α+β+γ).
For the moment, we shall regard this as the definition of the hyperbolic area.
the formula gives the expected result that area(ABC) = area(ACD)+area(BCD).
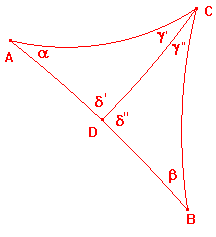
This follows from the diagram on the right.
ΔABC has angles α,β and γ = γ'+γ", so area(ABC)= π-(α+β+γ).
Also, area(ACD) = π-(α+δ'+γ'), area(BCD) = π-(δ"+β+γ").
Then area(ACD)+area(BCD) = 2π-(α+β+γ+δ'+δ") =π-(α+β+γ),
since δ'+δ" = π.
It follows that, if we divide a hyperbolic figure into hyperbolic triangles by adding
segments, and then add further segments to subdivide these triangles, then the
total area obtained will be the same. We then easily deduce that the area will be
independent of the triangulation, since we can use the segments of each of the
triangulations, and add more segments to produce a triangulation which refines
each of the original
ones.
In this way we can find the hyperbolic area of a hyperbolic polygon (i.e. a figure
bounded by hyperbolic segments which do not intersect except at their end points).
The restriction ensures that the figure has a well-defined interior. The simplest
case is that of a convex polygon, i.e. one in which the line from any interior point
to any vertex does not cross any side. If we choose an interior point and join it to
each vertex, then we have triangulated the polygon. We have essentially proved
the hyperbolic polygon theorem
If a convex hyperbolic polygon has n vertices, and interior angles α(1),...α(n), then
its hyperbolic area is (n-2)π-(α(1)+...+α(n)).
The -2 in the formula arises since tha angles round the interior point add up to 2π.
The figure on the right shows a convex hyperbolic pentagon (in red). The green
segments give the triangulation obtained from the interior point X.
In euclidean geometry, there are many ways to find the area of a triangle.
We will establish a hyperbolic analogue of one of these. We will also look at
other euclidean formulae. These lead to some interesting results, but not to
the hyperbolic area in any obvious way. We also consider hyperbolic circles.