Suppose that ABDC is a saccheri quadrialteral in the hyperbolic plane, having
right angles at C and D, and with d(A,C) = d(B,D) = d, d(C,D) = c, d(A,B) = a.
Let h be the length of the altitude of ABDC. Then
(1) sinh(½a) = cosh(d)sinh(½c),
(2) cosh(h)cosh(½a) = cosh(d)cosh(½c).
proof
(1) Let x = d(B,C), and let θ be the hyperbolic angle BCD.
Let M, N be the mid-points of AB, CD, so MN is the altitude.
We may as well move the picture so C,D lie on the real axis, as shown.
We have indicated the hypercircle XY on which A,B lie.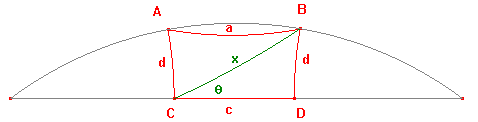
Then as ACD is a right angle, cos(ACB) = sin(θ).
We use various results on hyperbolic triangles.
By the Cosine Rule for ΔABC, cosh(a) = cosh(x)cosh(d)-sinh(x)sinh(d)sin(θ).
By the Sine Formula for ΔBCD, sin(θ) = sinh(d)/sinh(x).
By Pythagoras Theorem for ΔBCD, cosh(x) = cosh(c)cosh(d).
Combining these, cosh(a) = cosh(c)cosh2(d)-sinh2(d).
Using the formulae cosh(t) = 2sinh2(½t)+1, cosh2(d)-sinh2(d) = 1, we get
sinh2(½a) = cosh(2(d)sinh2(½c). The result follows.
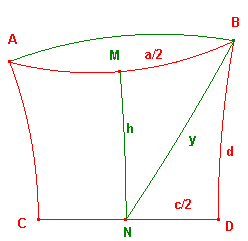
Let NB have hyperbolic length y.
By Pythagoras's Theorem applied to NDB, NMB, we get
cosh(y) = cosh(d)cosh(½c) = cosh(h)cosh(½a). The result follows.
Suppose that A,B lie on L, a hypercircle of width d associated with the hyperbolic
line H. Let C,D be the feet of the perpendiculars from A,B to H, and let a=d(A,B),
c=d(C,D). Then L, the hyperbolic length of the arc AB of L, satisfies
(1) L = cosh(d)c, and
(2) sinh(½a) = cosh(d)sinh(L/2cosh(d)).
proof
Finally, from the previous result, sinh(½a) = cosh(d)sinh(½c).
We may as well use the above picture.
Suppose we divide CD into N equal hyperbolic segments. Each has length c/N.
By the above result, the chord above each segment has length l, where
sinh(½l) = cosh(d)sinh(c/2N).
There are N chords, so the sum of their lengths is L*= Nl.
Thus sinh(L*/2N) = cosh(d)sinh(c/2N). Multiplying through by 2N, we get
2Nsinh(L*/2N) = cosh(d).2Nsinh(c/2N).
As N tends to infinity, L* tends to arc length, L and we get L= cosh(d)c.
Substituting for c, we get (2).