He considered a quadrilateral ABDC with right angles at C and D, and with CA
and DB of equal length. This is now called a saccheri quadrilateral.
He attempted to prove the Parallel Postulate by showing that the other angles
were also right angles. By assuming the contrary, he got results that were very
strange. We would now say that these are theorems of hyperbolic geometry.
A saccheri quadrilateral can be defined in neutral geometry since we require only
concepts of length and (right) angle.
The picture shows a hyperbolic example.
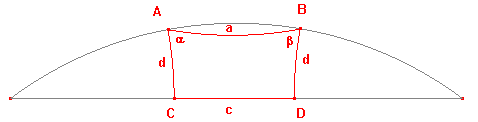
Notation
For the saccheri quadrilateral ABDC as above,
the base is the segment CD,
the base angles are those at C and D,
the summit is the segment AB,
the summit angles are those at A and B,
the sides are the segments AC and BD.
a neutral theorem on saccheri quadrilaterals
Suppose that S is a saccheri quadrilateral and let L be the
perpendicular
bisector of the base. Then
(1) L is an axis of symmetry of the quadrilateral,
(2) the summit angles are equal,
(3) L is the perpendicular bisector of the summit,
(4) L is the line joining the mid-points of the base and summit.
in view of (4), we refer to the segment joining the mid-points of the base
and summit as the altitude of the quadrilateral.
proof
Part (1) is simple since reflection in L maps the base to itself.
Then, as the base angles are equal, and the sides are of equal
length, the reflection maps the summit to itself, and hence S to S.
The other parts are easy consequences of the symmetry.
In euclidean geometry, the sum of the angles of any quadrilateral is 2π.
Since the base angles are ½π, and the summit angles are equal by (2)
above, the summit angles are also ½π so we have a rectangle. The
geometry of such figures is well-known!
In hyperbolic geometry, a saccheri quadrilateral ABDC has vertices A, B on a
hypercircle associated with a hyperbolic line H, and vertices C,D the feet of the
perpendiculars from A,B to H. This is the easy way to produce examples such
as that above. We have shown the hyperbolic line and the hypercircle.
a theorem on hyperbolic saccheri quadrialterals
Suppose that ABDC is a saccheri quadrialteral in the hyperbolic plane, having
right angles at C and D, and with d(A,C) = d(B,D) = d, d(C,D) = c, d(A,B) = a.
Let h be the length of the altitude of ABDC. Then
(1) sinh(½a) = cosh(d)sinh(½c),
(2) cosh(h)cosh(½a) = cosh(d)cosh(½c).
Note that, from (1), as cosh(d) > 1, a > c, i.e. the summit exceeds the base.
Then, from (2), h < d, i.e. the altitude is less than the side.
This leads to a formula for arc length along a hypercircle This is obtained by
approximating the arc by a sequence of hyperbolic segments.
arc length on a hypercircle
Suppose that A,B lie on L, a hypercircle of width d associated with the hyperbolic
line H. Let C,D be the feet of the perpendiculars from A,B to H, and let
a=d(A,B),
c=d(C,D). Then L, the hyperbolic length of the finite arc AB of L, satisfies
(1) L = cosh(d)c, and
(2) sinh(½a) = cosh(d)sinh(L/2cosh(d)).
This allows us to progress with showing a uniqueness theorem for
hyperbolic polygons.
There are other interesting results on saccheri quadrilaterals. For example, we can
give formulae for the summit angle and the hyperbolic area in terms of the lengths
of the base, sides and summit. Of course, the last is determined by the first two, as
we proved above. We discuss these in later pages.