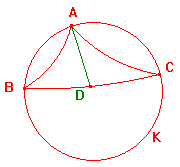
The point A lies oh the h-circle with h-diameter BC
if and only if <BAC = <ABC + <ACB.
Proof
Now suppose that <BAC = <ABC + <ACB.
Suppose first that BC is an h-diameter of the h-circle K with h-centre D.
Then d(D,A) = d(D,B) = d(D,C) (= h-radius of K).
By the Isosceles Triangle Theorem, applied to the h-triangles ABD and ACD,
we see that <ABC = <BAD, and <ACB = <DAC.
Thus <ABC + <ACB = <BAD +<DAC = <BAC.
This implies that <BAC is greater than <ABC,
so we can choose D on BC such that <BAD = <ABC.
Then as <BAC = <ABC + <ACB, <DAC =<ACB.
Again by the Isosceles Triangle Theorem, applied to ABD and ACD,
d(D,A) = d(D,B) = d(D,C), so A, B and C lie on an h-circle with
h-centre D, and BC is an h-diameter, since D is on BC.