many of the proofs mirror well-known euclidean proofs.
Basic stategy
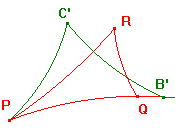
Suppose that ABC and PQR are h-triangles.
Then there is a hyperbolic transformation t which maps
A to P,
B to B' on the h-line PQ, on the same side of P as Q, and
C to C' on the same side of the h-line as R.
justification of basic strategy
Note that, as t preserves angle and hyperbolic distance,
d(A,B) = d(P,B'), d(A,C) = d(P,C'), d(B,C) = d(B',C'), and
<ABC = <PB'C', <BAC = <B'PC', <ACB = <PC'B'.
Our aim is to prove conditions which are sufficient for the
h-triangles to be h-congruent. In each case, we show that the
transformation t of the basic strategy actually maps B to Q,
and C to R, i.e. that B' = Q, and C' = R.
condition for congruence.
(SAS) condition
If h-triangles ABC and PQR have
then the h-triangles are h-congruent.
(1) d(A,B) = d(P,Q),
(2) <BAC = <QPR, and
(3) d(A,C) = d(P,R),
We use a common notation: (SAS) in the title refers to side, angle, side.
The order is significant, the angle is that enclosed by the pairs of sides.
Proof
Let t be the transformation implied by the Basic Strategy.
Then B' lies on the h-line PQ.
By the Basic Strategy, d(A,B) = d(P,B').
By (1), d(A,B) = d(P,Q), so d(P,B') = d(P,Q), and hence B' = Q.
By the Basic Strategy, <BAC = <QPC'.
By (2), <BAC = <QPR, so C' lies on PR.
By the Basic Strategy, d(A,C) = d(P,C').
By (3), d(A,C) = d(P,R), so d(P,C') = d(P,R), and hence C' = R.
Thus t maps ABC to PQR, so the h-triangles are h-congruent.
(ASA) condition
If h-triangles ABC and PQR have
then the h-triangles are h-congruent.
(1) <BAC = <QPR,
(2) d(A,B) = d(P,Q), and
(3) <ABC = <PQR,
In euclidean geometry, the sum of the angles of a triangle is constant.
Thus, if two triangles have two corresponding angles equal, then the
third angles must be equal. Thus (ASA) and (SAA) are equivalent in that
geometry. Here, however, we need a separate proof.
(SAA) condition
If h-triangles ABC and PQR have
then the h-triangles are h-congruent.
(1) d(A,B) = d(P,Q),
(2) <BAC = <QPR, and
(3) <ACB = <PRQ,
(SSS) condition
If h-triangles ABC and PQR have
then the h-triangles are h-congruent.
(1) d(A,B) = d(P,Q),
(2) d(A,C) = d(P,R), and
(3) d(B,C) = d(Q,R),
The final result is not true in euclidean geometry. There, two
triangles
with the corresponding angles equal need only be similar.
(AAA) condition
If h-triangles ABC and PQR have
then the h-triangles are h-congruent.
(1) <ACB = <PRQ,
(2) <ABC = <PQR, and
(3) <BAC = <QPR,
familiar, some strange looking.
The Isosceles Triangle Theorem
Suppose that ABC is an h-triangle.
(1) If d(A,B) = d(A,C) then <ABC = <ACB.
(2) If <ABC = <ACB then d(A,B) = d(A,C).
We choose a proof which illustrates the fact that the h-congruence
of two h-triangles involves an implicit correspondence between the
vertices. Thus, even if ABC is h-congruent to PQR, it is not usually
h-congruent to PRQ. In the proof, we meet the possibilty that we
may have ABC h-congruent to ACB.
proof of the isosceles triangle theorem
Of course, an h-triangle with either of these properties is called
an isosceles h-triangle.
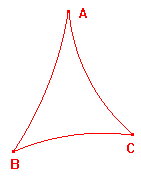
Note that such h-triangles do exist. The figure on the right was
produced by choosing B and C on an h-circle with h-centre A,
so that d(A,B) = d(A,C).
We can also define equilateral h-triangles as those
with three
equal sides (and hence three equal angles).
In euclidean geometry, the angle sum is π, so an equilateral
euclidean triangle has each of its angles equal to π/3.
In hyperbolic geometry, each angle must be less than π/3.
By the (AAA) condition, there is only one equilateral h-triangle
with angles equal to α for each α < π/3.
illustration of equilateral hyperbolic triangles
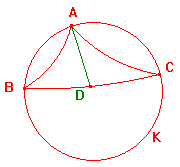
triangle in a semi-circle is always right-angled. One classical
proof adapts to hyperbolic geometry to yield
The Hyperbolic Semi-Circle Theorem
The point A lies on the h-circle with h-diameter BC
if and only if <BAC = <ABC + <ACB.
proof of the hyperbolic semi-circle theorem
The proof depends only on the Isosceles Triangle Theorem. This holds
in euclidean geoemtry, so our result is also a euclidean theorem. Of
course, in a euclidean triangle, the sum of the angles of a triangle is
equal to π. It follows that the angle at A must be π/2. Thus we can
recover the full euclidean result.