The Equal Angles Theorem

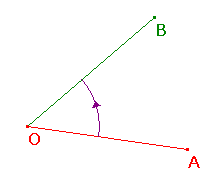
In inversive geometry, we shall generally regard angles as signed quantities. If OA and OB are segments, then there is a rotation about O taking A onto the ray OB. We regard this as defining the angle AOB (note the order of the letters). Obviously, this rotation is unique modulo 2p, so we may choose the unique value in the range (-p,p]. If a is the value in this range, then we say that the angle has magnitude |a|. Note that, if a and b have the same magnitude, then either b = a, or b = -a. If a is in (0,p), we say it has positive sense, the rotation is the anti-clockwise angle of magnitude a. If a is in (-p,0), we say it has negative sense. Note: since the rotations through ±p are identical, we cannot really attach a "sense" to p. With this definition, we clearly have <BOA = -<AOB.
To proceed, we need to look at the effect of inversion on angles.

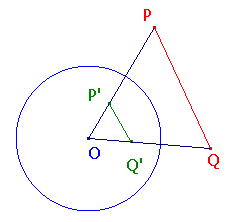
The Equal Angles Theorem Suppose that C is a circle with centre O, and that P and Q are points other than O. Let P and Q have inverses P' and Q' with respect to C. Then <QPO = <OQ'P' (in magnitude and sense)
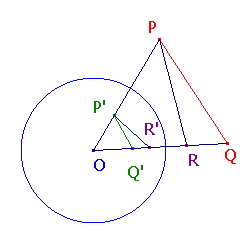
Corollary to the Equal Angles Theorem Suppose that P, Q and C are as in the theorem, and that R lies on the line OQ. Let R' be the inverse of R with respect to C. Then <QPR = -<Q'P'R' (in magnitude and sense) Proof of the Theorem and corollary We are now ready to look at the effect of inversion on lines and circles.

Main inversive page