


|  |
Orthogonal Curves
| In angles between arcs, we looked at the signed angle between two arcs meeting at a point.
Here, we will consider the magnitude of the angle(s) between two curves which meet at a point.
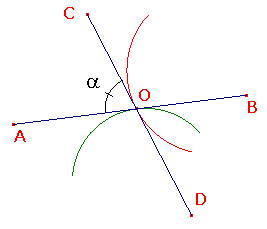
Suppose that, in the sketch, <AOC has magnitude a. Special case Suppose that the angle a is a right angle. Then all four angles round O are right angles. Definition Two intersecting curves are orthogonal if they meet at right angles.
|
 |
| Orthogonal lines and circles
Obviously, two lines are orthogonal if and only if they are perpendicular. Recall that, for a circle C, centre O, the tangent to C at a point P on C
In the CabriJava pane, you can drag P and watch the effect on |
|
| Now consider the case of two orthogonal circles C and D, with centres P and Q, meeting at A and B. Let L be the tangent to C at A, and M the tangent to D at A. Since the circles are orthogonal, L and M are perpendicular. As M is perpendicular to the tangent M to C, it passes through P, the centre of C. Similarly, L passes through Q, the centre of D. This is illustrated in the CabriJava pane on the right.
Observe that the tangent to C at B must also pass through Q.
The Uniqueness Theorem for Circles
If points A and B lie on a circle C, then there is a unique i-line
As you may guess, we can replace C by an extended line (so one of A, B may be Ñ).
|
|
|
The Uniqueness Theorem
If A and B are distinct points on an i-line L, then there is a unique i-line M
|
Since the proof is a good example
of the use of inversion, we give it in full. |
|
Proof
Since A and B are distinct, one of them (A say) is not Ñ. Note the structure of the proof.
We then get an algebraic version of the Invariance Theorem. This gives much more information about inversion. |
 |
| Main Inversive Page |