A parallel projection is an element of A(2).
Proof
Let f be the transformation which maps P in R3 to the
(1) f is a linear transformation.
(2) the algebraic form of t.
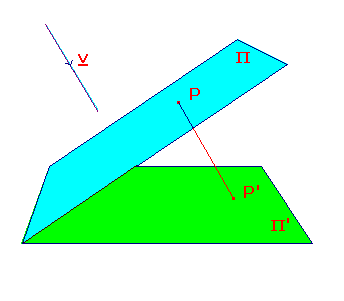
Suppose that t is the parallel projection from Π to Π'
along v, and that Π and Π' are equipped with axes.
We introduce axes for R3 by taking the x- and y-axes
of Π', and then the z-axis is the normal to Π', suitably
directed.
point where the line through P, parallel to v, meets Π'.
Thus, f maps R3 to R2. It is easy to see that t is the
restriction of f to Π.
Since v is not parallel to Π', the xy-plane in R3, its
z-component is non-zero. We may as well scale v so
that it is (m,n,1). The line through P(a,b,c) parallel to
v then has equation r = p + kv = (a+km,b+kn,c+k).
This meets Π' where c+k=0, i.e. k=-c, so that
f(a,b,c)=(a-cm,b-cn) - the image is on Π'. i.e. R2.
Thus f is linear.
Let A,B,C be the points on Π whose Π-coordinates are
(0,0),(1,0),(0,1), respectively, and let a, u and w be
the vectors OA, AB and AC.
Then the point P with Π-coordinates (α,β) has position
vector p = a + αu + βw.
Since f is linear, f(p) = f(a) + αf(u) + βf(w).
Since P is on Π, t(p) = f(p) = f(a) + αf(u) + βf(w).
Finally, f(a) + αf(u) + βf(w) = A(α,β)T+f(a),
where A is the matrix with columns f(u), f(w),
so that t is an element of A(2).