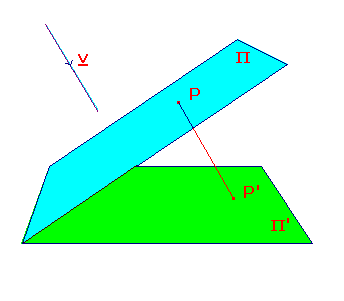
We introduce a family of transformations of the plane which turn out to generate the affine group A(2). The definition is purely geometric. It can be motivated by considering the relationship between all the shadows of an object. Definition If Π and Π' are planes in R3, and v is a vector not parallel to either, then parallel projection from Π to Π' along v is the map from Π to Π' mapping the point P on Π to P', the point where the line through P parallel to v cuts Π'. The definition of a parallel projection t from Π to Π' is purely geometrical. To obtain an algebraic description, we suppose that Π and Π' are each equipped with (rectangular) x- and y-axes. Then the transformation has a familiar form. Theorem A1 A parallel projection is an element of A(2). proof of theorem A1 Although every parallel projection is an affine transformation, not every affine transformation is a parallel projection. To see this, we can use the following Observation A parallel projection t preserves the lengths of segments of at least one line. Proof If the planes Π and Π' are parallel, then it is easy to see that the map t preserves the length of every segment. Otherwise Π and Π' meet in a line L. The points of L are fixed pointwise by t, so the length of every segment of L is fixed. Now note that the dilation about O with scale factor 2 doubles the length of every segment. This is the affine transformation taking x to 2Ix+0. Thus, we have an affine transformation which is not a parallel projection. However, we can obtain any affine transformation by composing parallel projections: Theorem A2 The affine group A(2) is generated by parallel projections. proof of theorem A2

main affine page