The affine group A(2) is generated by parallel projections.
Proof
Suppose that t is an affine transformation which maps the
We will define two parallel projections which have the same
We begin by taking 3 copies Π, Π' and Π" of the plane.
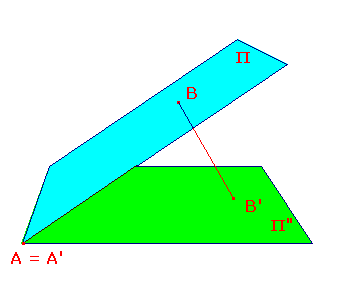
First, we place Π and Π" so that the point A on Π
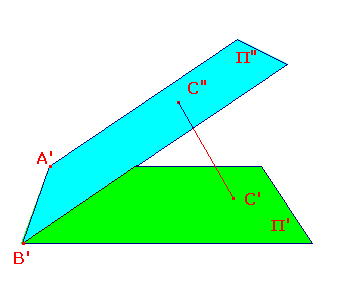
Now place Π" and Π' so that the points A', B' coincide.
Thus qop maps A, B, C to A', B', C'. By Theorem A1, the
We use the Fundamental Theorem of Affine Geometry,
which shows that an affine transformation is uniquely
determined by the images of three non-collinear points.
non-collinear points A, B, C to the (non-collinear) points
A', B', C', respectively.
effect on A, B and C.
On Π, we mark the points A, B and C.
On Π' and Π", we mark the points A', B' and C'.
coincides with A' on Π". By rotating the planes about
this point, we can ensure that neither B nor B' lies on
the line of intersection. Then u = BB' is not parallel to
either plane, so we can define the parallel projection p
from Π to Π" along u. This maps A to A', and B to B'.
Suppose that it maps C to C". Since A, B, C are not
collinear, their images A', B', C" are not collinear.
As neither C' nor C" is collinear with these, they do not
lie on the line of intersection. Thus v = C'C" is not
parallel to either plane, so we can define the parallel
projection q from Π" to Π' along v. This fixes A' and B',
and maps C" to C'.
maps p and q are affine, so the composite is also affine.
Since t and qop have the same effect on three points,
the Fundamental Theorem shows that they are equal.