of betweenness. Given three collinear points, one lies between the
other two. This is preserved by the appropriate transformations.
The concept of line segment is based on betweenness.
In projective geometry, there is no corresponding concept.
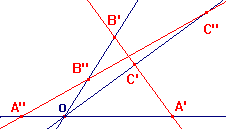
Suppose that A,B,C are collinear p-points. They are represented
by three coplanar lines through O. Imagine that they lie in the
plane of the screen. In a general embedding, the representatives
of A,B,C are collinear points. In the sketch, these are the red lines
A'B'C' and A"B"C". Observe that C' lies between A' and B', while
B" lies between A" and C". Thus, there is no sensible way to say
that one of A,B,C lies between the other two.
by two p-points on the p-line. As a consequence, the definition of
a triangle in projective geometry is rather different from that in
the other geometries. If A,B,C are non-collinear p-points, then the
sides of ΔABC are the (complete) p-lines AB, BC and CA. Given
three distinct p-lines, L,M,N, these define a triangle with vertices
the intersections of the p-lines in pairs.
that of the interior of a triangle. The sides of a projective triangle
are represented by three planes through O. These divide space
into eight regions. There is no consistent way to choose any one
of these as the interior.
example
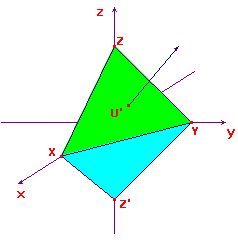
In Π, the vertices embed as X(1,0,0), Y(0,1,0), Z(0,0,1).
In Φ, the vertices embed as X, Y and Z'(0,0,-1).
Consider the projective triangle Δ with vertices [1,0,0], [0,1,0]
and [0,0,1]. These are representd by the coordinate axes.
The sides are represented by the coordinate planes.
The point P[1,1,1] does not lie on any side of the triangle.
We
shall look at the embedding in two different planes.
Let Π be the plane x+y+z = 1, and Φ the plane x+y-z = 1.
A simple calculation shows that P embeds as U'(1/3,1/3,1/3).
This lies in the triangle XYZ shown in green in the sketch.
By direct calculation, P embeds as U(1,1,1).
The triangle XYZ' on Φ (shown in cyan) does not contain U.
On the other hand, we can define the interior of a projective conic
in a way consistent with the projective group.