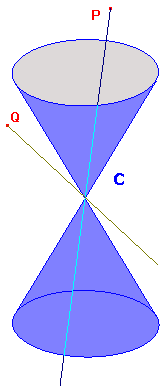
and a p-point P as a line through O. Intuitively, P lies inside C if the
angle the line makes with the axis is less than the semi-vertical
angle of the cone, and outside otherwise. The sketch on the right
shows P inside the cone, and Q outside.
Unfortunately, neither the axis nor the semi-vertical angle are preserved
by projective transformations. The latter is obvious, since all cones are
projective congruent. The former will become clear when we see that it is
possible to map C to C in such a way that a given interior p-point maps
to
any other interior p-point.
We require a characterization in terms of projective concepts. We begin
by looking at alternative intuitive descriptions, and derive a suitable
formal definition.
First of all, we note that a p-line meets a p-conic at most twice, since
the p-line has a linear equation and the p-conic a quadratic equation.
Thus the p-line is a tangent if it meets the p-conic in just one p-point.
If P is a p-point lying inside C in the above sense, then any
p-line which
passes through P meets
C twice. It follows from the above remark that
there are no tangents to C through P.
If Q is a p-point lying outside C in our intuitive sense, then it is clear
that there are p-lines through Q which meet C twice, and p-lines which
do not meet C. By considering a p-line (a plane) rotating round Q, we
see that there are two tangents through Q - one where the p-line first
meets C, and one where it meets it for the last time. We believe that
this is intuitive, but we will give a formal proof later.
Suppose that C is a p-conic, and P a p-point. Then
P lies inside C if there is no tangent to C through P, and
P lies outside C if there are (at least) two tangents to C through P.
Of course, if a p-point T lies on C, then there is one tangent through T,
namely
the tangent at T.
The Corollary to the Invariance Theorem shows that for any
projective transformation t, maps tangents to C through P correspond to
the tangents to t(C) through t(P). Thus, the number of tangents is
the same for P and for t(P). This proves
The interior-exterior theorem of projective geometry
If C is a p-conic and t a projective transformation, then t maps
the interior of C to the interior of t(C), and
the exterior of C to the exterior of t(C).
We now require one of the most significant results of projective geometry.
This allows us to describe the interior and exterior of a p-conic in terms
of polars.
La Hire's Theorem
If C is a p-conic, and P, Q are p-points, then
Q lies on the polar of P if and only if P lies on the polar of Q.
Note that, if T lies on the p-conic C, then the polar of T with respect to C
is the tangent at T. Now suppose that the tangent at T passes through the
p-point P. Then P lies on the polar of T, so, by La Hire's theorem, T lies on
the
polar of P. But T lies on C, so the polar of P meets C - at T.
Immediately, we
see that, if P lies inside C, then there are no tangents
through P, so that the polar of P does not meet C.
If there is one tangent through P, then the polar of P meets C just once,
i.e. is a tangent to C, at T, say. The polar
of T is this same tangent, so we
must have P=T, i.e. P lies on C.
Finally, suppose that there are at least two tangents through P, and that
two of them meet C at S and T. Then the polar of P meets C at S and T.
The polar is a p-line, so meets C at most twice.
These remarks justify the earlier assertion that a p-point outside C lies
on exactly two tangents. They also prove
the polar characterization of interior and exterior
Suppose that C is a p-conic, and that L is the polar of the p-point P. Then
P lies inside C if and only if L does not meet C,
P lies on C if and only if L meets C once, and
P lies ouside C if and only if L meets C twice.
We can also characterize the interior in terms of the equation of the
projective conic. Since this leads us in a new direction, we shall give it on
a separate page.
We are now in a position to look at the effect of projective symmetries of
a p-conic on the interior and exterior. We will get a two-point theorem,
but first, we must look at the projective symmetry group of a conic.