cone with vertex O. If Π is a plane not through O, then the embedding
of C consists of the intersection of the cone and plane, plus any ideal
points for Π contained in C. Of course, the ideal points arise from any
intersections of C with the plane Π* through O parallel to Π since Π*
corresponds to the ideal line in the embedding. The intersection of C
and Π is a (non-degenerate) plane conic, which we shall call C(Π).
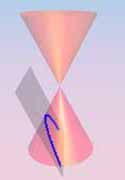
Observe that C(Π) will be a parabola precisely when the plane Π is
parallel to a generator L of C. Then Π* will be the tangent (plane)
to C, meeting it in L. In the language of RP2, Π* is the p-line which
is tangent to the p-conic C at the p-point L. In the embedding, we
note that Π* corresponds to the ideal line, and L (which lies in Π*)
to an ideal point. Thus, for a parabola, the ideal line is a tangent at
the (unique) ideal point on the embedding.
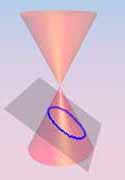
For an ellipse, the plane Π* does not meet C, so there are no ideal
points on the embedding.
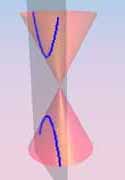
For a hyperbola, Π* cuts C twice, and we have two ideal points. The
directions these define are those of the asymptotes (which in turn
correspond to the tangents at these ideal points).
All of this is discussed in detail in the
projective geometry pages.
On the right are picutres illustrating the ideas. These pictures
do not show Π*, but is easy enough to imagine it since it is the
plane through the vertex, and parallel to the cutting plane.
We can reverse this process. If we are given the plane conic C'
with equation ax2+bxy+cy2+fx+gy+h=0, then we can regard C'
as lying on the plane Π : z=1. Note that Π* is the plane z=0.
Then the p-conic C : ax2+bxy+cy2=fxz+gyz+hz2=0 is such that
C' = C(Π). The ideal points on the embedding of C correspond
to the intersections of C with Π*, i.e to the solutions (if any) of
the equation ax2+bxy+cy2 = 0.