The circle C : x2+y2-2ax-2by+c = 0 is orthogonal to the circle C : x2+y2 = 1
if and only if c = 1 and a2+b2 > 1.
Proof
Suppose that C has centre P(a,b) and radius r, then the condition becomes
We immediately deduce that a2+b2 > 1, and that C
must have the equation
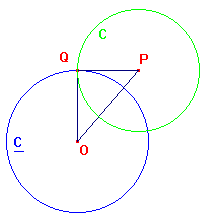
The circles C and C are orthogonal if and only if the tangents at the points of
intersection are perpendicular. Suppose that the circles have centres P and O,
and that they meet at Q. Then it is easy to see that the circles are orthogonal
if and only if the radii OQ and PQ are perpendicular. Applying Pythagoras, we
see that this occurs if and only if |OQ|2+|QP|2 = |OP|2.
1+r2 = |OP|2 = a2+b2,
i.e. r2 = a2+b2-1.
(x-a)2+(y-b)2 = r2 = a2+b2-1, i.e.
x2+y2-2ax-2by+1 = 0, so we need c = 1.