Suppose that we define a geometry as a set S and a group G. Another geometry
with set S' and group G' is essentially the same as this if the points of S' are in
one-one correspondence with the points of S in such a way that the action of G'
on S' corresponds to the action of G on S. In such a case, we say that we have
two models of the geoemtry, defined on S and on S'.

Formally, we require a bijection k from S to S', so that the sets correspond. We
also want the actions of the groups G and G' to correspond. Suppose that PεS and
that gεG with g(P) = Q. The element g' of G'corresponding to g must send k(P)
to k(Q), i.e. we must have g'ok(P) = k(Q) = kog(P). Since we require this for all
P and g, we require that G' = kGk^-1.

Observe that, if we know S, S' and the bijection k, then we can obtain a model on
the set S' simply by defining the group G' as kGk^-1.

Finally, if the geometry on S has "lines", then we can define the "lines" in S' as the
subsets {k(L) : L is a "line" in S}. Of course, the lines in S' will enjoy geometrical
properties identical to those in S. But note that the two sets of "lines" may look
different, i.e. may have different euclidean properties.

We introduced hyperbolic geometry using the poincare disk model, whose set is the
unit disk D and whose group is H(2). The hyperbolic lines are arcs of euclidean circles
rather than line segments.The advantage is that the angles between hyperbolic lines
are represented by the euclidean angles between the euclidean tangents to the arcs.

There are other models, each with their own useful features. We shall consider two.

To relate the models to the poincare disk, we need an algebraic description of when
two circles are orthogonal.

Lemma
The circle C : x²+y²-2ax-2by+c = 0 is orthogonal to the circle C : x²+y² = 1
if and only if c = 1 and a²+b² > 1.

proof

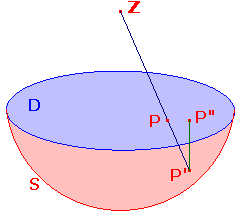
the klein (or klein-beltrami) model The set is D, as for the poincare model. It is defined by a bijection k from D, regarded as the set of the poincare model, to D, regarded as the set of our new model. Regard D as lying on the xy-plane in three-dimensional space. Let S denote the lower half of the sphere x2+y2+z2 = 1, S = {(x,y,z) : x2+y2+z2 = 1, z < 0} The map k is defined in two stages: project each point P on D stereographically from Z(0,0,1) onto S, i.e. map P to P', the point where the line ZP cuts S. project P' orthogonally onto D, i.e. to the point P" on D lying vertically above P". Note that the points of D lie on the xy-plane, and we view the final map k as a two-dimensional map, i.e. we suppress the z-coordinate which is always 0. As above, the group is kH(2)k-1, though it is difficult to describe explicitly. The k-lines are the subsets of the form k(H), where H is an h-line. We find that these have a particularly simple form - in some ways, nicer than the h-lines. The Poincare-Klein Map The map k is given by k(x,y) = (2x/(1+x2+y2),2y/(1+x2+y2)). The map k maps the h-line with boundary points AB to the intersection of the euclidean line AB with D. The inverse is k-1(x,y) = (x/1+(1-x2-y2)½,y/1+(1-x2-y2)½). proof Thus, the k-lines are the intersections of D with euclidean lines - i.e. are euclidean segments. A number of properties of hyperbolic geometry are easy to prove using this model. For example if P and Q lie in D, then there is a unique k-line throgh P and Q. two k-lines meet in at most one point. We can also prove results which are hard to tackle in the poincare model. Pappus's Theorem in Hyperbolic Geometry Suppose that A,B,C lie on a hyperbolic line L, and A',B',C' on a hyperbolic line L'. If the hyperbolic lines AB',A'B meet in P, BC',B'C in Q and CA',C'A in R, then the points P,Q,R are collinear. In the klein model, the hyperbolic lines are euclidean segments. The euclidean version of Pappus's Theorem applies to the diagram, and this then proves the hyperbolic version!
the minkowski model This model has as its set a certain surface in three-dimensional space. A point (x,y,z) on the hyperboloid x2+y2-z2=-1 has z2 = 1+x2+y2 ≥ 1, so z ≥ 1 or z ≤ -1. Thus the hyperboloid consists of two sheets on either side of the xy-plane. We take as our set H the sheet with z ≥ 1. This is discussed further in the hyperboloid page. We map D to H by stereographic projection from Z'(0,0,-1). This gives the map m. The proof of the following result shows that m is actually a bijection between the sets. The Poincare-Minkowski Map The map m is given by m(x,y) = (2x/(1-x2-y2),2y/(1-x2-y2), (1+x2+y2)/(1-x2-y2)). The map m maps an h-line to the intersection of H with a plane through O. The inverse is given by m-1(x,y,(1+x2+y2)½) = (x/(1+(1+x2+y2)½), y/(1+(1+x2+y2)½). proof The minkowski model has the set H. The m-lines are the intersections of H with planes through the origin. This model is related to special relativity. It is also of considerable significance in geometry. The group for the minkowski model is isomorphic to a subgroup of the projective group P(2). This shows that hyperbolic geometry is related to projective geometry. Unfortunately, the proof of the isomorphism is rather complicated. By the above theory the group of the minkowski model is mH(2)m-1. The Hyperbolic-Projective Theorem If m is the bijection from the hyperbolic model to the minkowski model, and K the projective conic with equation x2+y2-z2 = 0, then the group mH(2)m-1 is isomorphic to the projective symmetry group of K. proof

main klein page