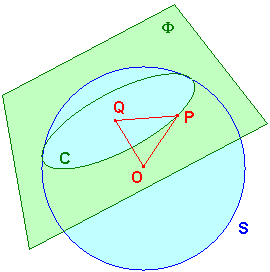
If a plane F cuts a sphere S non-trivially,
then the intersection is a circle.
Suppose that the point P lies on C, the curve of intersection.
Let Q be the foot of the perpendicular to F from O, the centre of S.
Then DOPQ is right-angled at Q.
Hence OP2 = OQ2 + QP2, so that QP2 = OP2 - OQ2.
But OP is the radius of S, and OQ is the distance from O to F,
so are constant. Thus QP is constant, so C is a circle.