


|  |
Stereographic Projection - an alternative approach to the extended plane and i-lines
| The material on these pages gives an alternative approach to the introduction of the point at infinity and the concepts of extended lines and i-lines. It is not used to prove any results not proved elsewhere.
Since the World is approximately spherical, geographers have
The easiest solution is to use a projection map. We shall look at stereographic projection.
Definition
In the sketch, we have taken N as the North Pole of the sphere,
Note that the changing P merely changes the scale of the resulting
If we choose Q on P, then the line NQ cuts S-{N} exactly once.
|
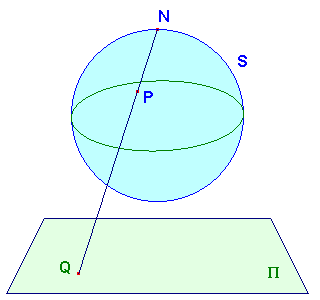 |
| The map p is so far defined only on S -{N}. To extend it to all of S, we introduce the extended plane P+=P+{Ñ}, where Ñ is called the point at infinity. We say that p(N) = Ñ.
Now p gives a bijection from S to P+{Ñ}.
|
See The Extended Plane for an alternative approach |
| Circles on S
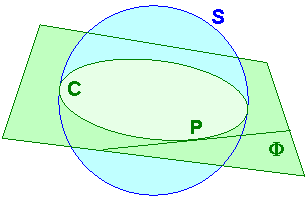
Let F be a plane which cuts S non-trivially.
Although we shall not pursue it far, there is a geometry on S If P is a point on C, then there is a tangent to C at P. This lies in F.
|
 |
Definition
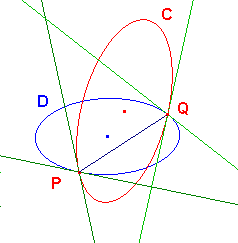
If C and D are circles on S meeting in P, then the
Of course, the circles will in general meet again, at Q say.
If we view the picture looking in towards the centre of the sphere,
We now prove two theorems which together show that
|
 |
|
Theorem 1
Let p denote stereographic projection with vertex N
from
Theorem 2
Stereographic projection preserves angles.
|
| Main inversive page |