proofs of facts about half-turns

facts about half-turns

  1. A half-turn about the point C with position vector c is r(x) = 2c - x.
  2. The transformation r(x) = b - x is a half-turn about the point ½b.
  3. The composite of two half-turns is a translation.
proofs
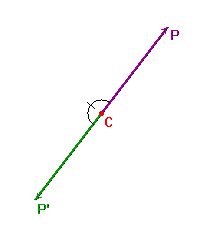
(1) Suppose that the point P has image P' = r(P), and that these points have
position vectors x and x', respectively. Then, as r is a half-turn about C,
CP' = -CP, i.e. x' - c = -(x - c) = c - x, so that x' = 2c - x.
(2) follows immediately from (1).
(3) Supose that r and r' are the half-turns. then, by part (1), r(x) = b - x
and r'(x) = b' - x, for some vectors b and b'. Composting these, we have
ror'(x) = r(b' - x) = b - (b' - x) = x + (b - b'). Thus ror' is the translation
by the vector (b - b').

half-turns page