When we write the equation of an ellipse or hyperbola C in standard form
we see that the transformation r((x,y)) = (-x,-y) maps C to itself. This
transformation is a rotation about the origin through angle π, a half-turn.
The existence of a half-turn mapping a conic to itself has many interesting
consequences. We begin by looking at the half-turn about a general point.
facts about half-turns
proofs of these facts
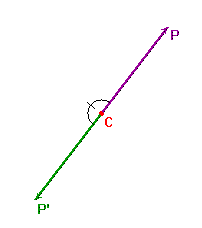
The point C which is fixed by a half-turn r is the centre of r.
From the definition of a half-turn as a rotation, it clearly belongs to E(2), the
euclidean group. Of course, it also belongs to the larger groups S(2) and A(2).
An element t of the affine group A(2) has the from t(x) = Ax + b, where
A is a non-singular matrix and b a vector. We shall call this A the matrix of t.
As an element of A(2), a half-turn has the form r(x) = (-I)x + b.
In affine
geometry, we do not have the concept of angle, so we take as the definition
of a half-turn the property that the matrix is -I. The centre is ½b. It is clearly
the only fixed point of r.
The affine half-turn theorem
If r is the half-turn with centre C, and t is any affine transformation,
then torot-1 is the half-turn with centre t(C).
Definitions
(1) A plane conic is central if it is an ellipse or hyperbola.
(2) The centre of a central conic is the centre of the half-turn in the symmetry group.
(3) A diameter of a central conic is a line which passes through the centre.
Note that the centre is well defined since a half-turn is a euclidean transformation,
and we know that the euclidean symmetry group of such a conic contains only one.
From the affine half-turn theorem, we can deduce
The central conic theorem
If C is a central conic, with centre C, and t is an affine transformation,
then t(C) is central, with centre t(C).
The centre of a conic is thus an affine concept. Suppose that t belongs to the affine
symmetry group of a central conic C, with centre C. Then t(C) = C. By the theorem,
t(C) has centre t(C), so t(C) = C. Thus, every affine symmetry of C fixes C. Note that
the fixed point theorem does not apply, since the affine symmetry group of a conic
is infinite, as we shall shortly see.
The centre and diameters have many interesting properties. Some of the nicest
will be obtained in a unifed way for all conics - including parabolas which do not
appear to have a centre. This involves projective ideas.
For the moment, we give just one example.
The central property
If C is a central conic with centre C, and A is any point on C,
then AC meets C again at B, and C is the mid-point of AB.