geometrical. It does not depend on the choice of axes in the planes
Π and Π'. Further, the perspectivity is determined by the images of
the points of Π which have images on Π' - this excludes, at most, a
single line L on Π. The images of points on L, and of the ideal points
for Π follow as on the previous page.
The projective group P(2) of transformations of RP2 consists of
mappings of the form t([x]) = [Ax], where A is a non-singular 3x3
real matrix.
To relate the extended plane and RP2 models of the projective plane,
we placed the euclidean plane E on the plane z=1. Then there is a
one-one correspondence between RP2 and the extended plane Ê.
We refer to this as an embedding of
RP2 in z=1. We could equally well
choose to place E on any plane not through the origin to get an
embedding in the appropriate plane.
This allows us to interpret a perspectivity as a transformation of RP2.
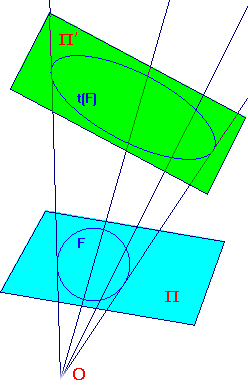
Suppose that t is the perspectivity from Π to Π' with vertex O.
We choose a plane Φ not through the origin in R3.
Then we obtain
two embeddings of RP2 by placing Π and Π' respectively on the plane Φ.
The perspectivity t maps points of the extended plane Π to points of
the extended plane Π'. Since points of these extended planes are now
regarded
as elements of RP2, we have a transformation of RP2.
Obviously, the above transformation will depend on the choice of Φ.
To obtain a transformation which belongs to P(2), We choose axes
with O, the vertex of t, as origin. we then Π itself as the embedding
plane i.e. take Φ = Π. Now, to place Π' in the position Π, we can use
(1) a rotation about O, mapping &Pi'; to Π*, parallel to Π, and then
(2) parallel projection of Π* to Π along the common normal.
Observe that each is a linear transformation, so that their combined
effect is a linear transformation t*, with matrix A, say.
Also, the transformation t* maps Π' rigidly onto Π.
Suppose that F is a figure on Π. Then, as Π is the embedding plane,
the corresponding figure F' in RP2 consists of all rays through the
points of F. These rays meet Π' in the points of t(F), so we can also
regard F' as the set of rays through points of t(F).
The mapping t*
takes t(F) to an exact copy F* on Π.
Again since Π
is the embedding plane, the image in RP2 consists of rays through
points of F*. Since t* is linear, it maps the p-points through F to the
p-points through F*, which is isomorphic to t(F). Thus the mapping
taking [x] to [Ax] corresponds to the perspectivity t.
Lemma 1
A perspectivity defines an element of P(2).
Of course, the element of P(2) will depend on the choice of the
(common) embedding plane for the planes of the perspectivity.
An element of P(2) can be expressed as a composite of
at most three maps obtained from perspectivities. This can be stated as "the group P(2) is generated by perspectivities".
return to main perspectivities page